7.1.4.1. XSProc: Standard Composition Examples
7.1.4.1.1. Standard composition fundamentals
The standard composition specification data are used to define mixtures using standardized engineering data entered in a free-form format. The XSProc uses the standard composition specification data and information from the Standard Composition Library to provide number densities for each nuclide of every defined mixture according to Eq. (7.1.1).
where
NO is the number density of the nuclide in atoms/b-cm,
RHO is the actual density of the nuclide in g/cm3,
AVN is Avogadro’s number, 6.02214199 \(\times\) 1023, in atoms/mol,
C is a constant, 10-24 cm2/b,
AWT is the atomic or molecular weight of the nuclide in g/mol.
The actual density, RHO, is defined by
where
RHO is the actual density of the standard composition in g/cm3,
ROTH is either the specified density of the standard composition or the theoretical density of the standard composition in g/cm3,
VF is a density multiplier compatible with ROTH as defined by Eq. Eq. (7.1.3),
WGTF is the weight fraction of the nuclide in the standard composition. This value is automatically obtained by the code from the Standard Composition Library. WGTF is 1.0 for a single nuclide standard composition.
where
VF is the density multiplier,
DFRAC is the density fraction,
VFRAC is the volume fraction.
To illustrate the interaction between ROTH and VF, consider an Inconel having a density of 8.5 g/cm3. It is 7.0% by weight iron, 15.5% chromium, and 77.5% nickel. The Inconel occupies a volume of 4 cm3.
Method 1:
To describe the iron, enter 8.5 for ROTH and 0.07 for VF.
To describe the chromium, enter 8.5 for ROTH and 0.155 for VF.
To describe the nickel, enter 8.5 for ROTH and 0.775 for VF.
Method 2:
Do not enter the density, and by default the theoretical density of each component will be used for ROTH. DFRAC will be the ratio of the specified density to the theoretical density. The specified density of each component is the density of the Inconel \(\times\) the weight fraction of that component.
Thus, the density of the iron is 8.5 \(\times\) 0.07 = 0.595 g/cm3
chromium is 8.5 \(\times\) 0.155 = 1.318 g/cm3
nickel is 8.5 \(\times\) 0.775 = 6.588 g/cm3.
To calculate DFRAC, the theoretical density of each material must be obtained from the table Elements and special nuclide symbols in the STDCMP chapter. These values are
7.86 g/cm3 for iron
8.90 g/cm3 for nickel
7.20 g/cm3 for chromium
The DFRAC entered for the iron is 0.595/7.86 = 0.0757
for the nickel is 1.318/8.90 = 0.1481
for the chromium is 6.588/7.20 = 0.9163.
Since there are no volumetric corrections, VFRAC is 1.0 and the values of DFRAC are entered for VF.
Method 3:
Assume the Inconel, which occupies 4 cm3, is to be spread over a volume of 5 cm3. Then the volume fraction, VFRAC, is 4 cm3/5 cm3 = 0.8 and can be combined with the density fraction, DFRAC, to obtain the density multiplier, VF.
To describe the iron, enter 8.5 for ROTH and 0.07 \(\times\) 0.8 = 0.056 for VF
To describe the chromium, enter 8.5 for ROTH and 0.155 \(\times\) 0.8 = 0.124 for VF
To describe the nickel, enter 8.5 for ROTH and 0.775 \(\times\) 0.8 = 0.620 for VF.
Alternatively, the volume fraction can be applied to the density before it is entered. Then the ROTH can be entered as 8.5 g/cm3 \(\times\) 0.8 = 6.8 g/cm3, and DFRAC is entered for the density multiplier, VF.
To describe the iron, enter 6.8 for ROTH and 0.07 for VF
for chromium, enter 6.8 for ROTH and 0.155 for VF
for nickel, enter 6.8 for ROTH and 0.775 for VF.
Method 4:
Assume the Inconel, which occupies 4 cm3, is to be spread over a volume of 5 cm3. Then the volume fraction, VFRAC, is 4 cm3/5 cm3 = 0.8. Do not enter the density, and by default the theoretical density of each component will be used for ROTH.
VF is then entered as the product of VFRAC and DFRAC according to Eq. . The specified density of each component is the density of the Inconel \(\times\) the weight fraction of that component.
Thus, the density of the iron is 8.5 \(\times\) 0.07 = 0.595 g/cm3
Chromium is 8.5 \(\times\) 0.155 = 1.318 g/cm3
Nickel is 8.5 \(\times\) 0.775 = 6.588 g/cm3.
To calculate DFRAC, the theoretical density of each material must be obtained from Table 7.2.3. These values are
7.86 g/cm3 for iron 8.90 g/cm3 for nickel 7.20 g/cm3 for chromium.
Then DFRAC for the iron is 0.595/7.86 = 0.0756
for nickel is 1.318/8.90 = 0.1481
for chromium is 6.588/7.20 = 0.9150.
Then VF is DFRAC \(\times\) VFRAC
VF for the iron is 0.0757 \(\times\) 0.8 = 0.0606
for nickel is 0.1481 \(\times\) 0.8 = 0.1185
for chromium is 0.9150 \(\times\) .8 = 0.7320.
7.1.4.1.2. Basic standard composition specifications
EXAMPLE 1. Material name is given. Create a mixture 3 that is Plexiglas.
Since no other information is given, the information on the Standard Composition Library can be assumed to be adequate. Therefore, the only data to be entered are the standard composition name and the mixture number
PLEXIGLAS 3 END
EXAMPLE 2. Material name and density (g/cm3) are given.
Create a mixture 3 that is Plexiglas at a density of 1.15 g/cm3. Since no other data are specified, the defaults from the Standard Composition Library will be used. Therefore, the only data to be entered are the standard composition name, the mixture number, and the density.
PLEXIGLAS 3 DEN=1.15 END
EXAMPLE 3. Material name and number density (atoms/b-cm) are given. Create a mixture 2 that is aluminum having a number density of 0.060244.
AL 2 0 .060244 END
EXAMPLE 4. Material name, density (g/cm3) and isotopic abundance are given.
Create a mixture 1 that is uranium metal at 18.76 g/cm3 whose isotopic composition is 93.2 wt % 235U, 5.6 wt % 238U, and 1.0 wt % 234U, and 0.2 wt % 236U. This example uses the DEN= keyword to enter the density and define the standard composition. Example 5 demonstrates another method of defining the standard composition.
URANIUM 1 DEN=18.76 1 300 92235 93.2 92238 5.6 92234 1.0 92236 0.2 END
EXAMPLE 5. Material name, density (g/cm3) and isotopic abundance are given.
Create a mixture 7 defining B4C with a density of 2.45 g/cm3. The boron is 40 wt % 10B and 60 wt % 11B. This example utilizes the DEN= keyword. Example 6 illustrates an alternative description.
B4C 7 DEN=2.45 1.0 300 5010 40.0 5011 60.0 END
EXAMPLE 6. Material name, density (g/cm3) and isotopic abundance are given.
Create a mixture 7 defining B4C with a density of 2.45 g/cm3. The boron is 40 wt % 10B and 60 wt % 11B. This example incorporates the known density into the density multiplier, vf, rather than using the DEN= keyword. The default density for B4C given in the COMPOUNDS table in the SCL section 7.2 is equal to 2.52 g/cm3.
B4C 7 0.9722 300 5010 40.0 5011 60.0 END
Note
In the above examples, the actual density is input for materials containing enriched multi-isotope nuclides (uranium in Examples 4 and 5 and boron in Examples 6 and 7). The default density should never be used for enriched materials, especially low atomic mass neutron absorbers such as boron and lithium. The default density is a fixed value for nominal conditions and naturally occurring distributions of isotopes. Use of the default density for enriched materials will likely result in incorrect number densities
7.1.4.1.3. User-defined (arbitrary) chemical compound specifications
The user-defined compound option allows the user to specify materials that are not found in the Standard Composition Library and can be specified by the number of atoms of each element or isotope that are contained in the molecule. To define a user-defined compound, the first four characters of the standard composition component name must be ATOM. The remaining characters of the standard composition component name are chosen by the user. The maximum length of the standard composition name is 16 characters. All the information that would normally be found in the Standard Composition Library must be entered in the user-defined compound specification. Sect. 7.1.3.3 contains data input details for arbitrary compounds.
EXAMPLE 1. Density and chemical equation are given.
Create a mixture 3 that is a hydraulic fluid, C2H6SiO, with a density of 0.97 g/cm3. The input data for this user-defined compound are given below:
ATOM 3 0.97 4 6000 2 1001 6 14000 1 8000 1 END
EXAMPLE 2. Density and chemical equation are given. Create a mixture 7, TBP, also known as phosphoric acid tributyl ester or tributylphosphate, (C4H9O)3PO, having a density of 0.973 g/cm3.
ATOMtbp 7 0.973 4 1001 27 6000 12 8016 4 15031 1 end
7.1.4.1.4. User-defined (arbitrary) mixture/alloy specifications
The user-defined compound or alloy option allows the user to specify materials that are not found in the Standard Composition Library and are defined by specifying the weight percent of each element or isotope contained in the material. To define a user-defined weight percent mixture, the first four characters of the standard composition component name must be wtpt. The remaining characters of the standard composition component name are chosen by the user. The maximum length of the standard composition name is 16 characters. All the information that would normally be found in the Standard Composition Library must be entered in the arbitrary mixture/alloy specification. Sect. 7.1.3.3 contains data input details for user-defined compounds.
EXAMPLE 1. Density and weight percents are given.
Create a mixture 5 that defines a borated aluminum that is 2.5 wt % natural boron. The density of the borated aluminum is 2.65 g/cm3.
SOLUTION MIX=2 RHO[UO2(NO3)2]=415 92235 92.6 92238 5.9 92234 1 92236
0.5 MASSFRAC[HNO3]=6.339-6 TEMPERATURE=293 END SOLUTION
EXAMPLE 2. Density, weight percents, and isotopic abundance are given.
Create a mixture 5 that defines a borated aluminum that is 2.5 wt % boron. The boron is 90 wt % 10B and 10 wt % 11B. The density of the borated aluminum is 2.65 g/cm3. The minimum generic input specification for this arbitrary material is
WTPTBAL 5 2.65 2 5000 2.5 13027 97.5 1 293 5010 90. 5011 10. END
7.1.4.1.5. Fissile solution specifications
Solutions of fissile materials are available in the XSProc. A list of the available solution salts and acids is given in the table Available fissile solution components in Sect. 7.2.3. When the XSProc processes a solution, it breaks the solution into its component parts (basic standard composition specifications) and uses the solution density to calculate the volume fractions.
EXAMPLE 1. Fuel density, excess acid and isotopic abundance are given.
Create a mixture 2 that is a highly enriched uranyl nitrate solution with 415 g/L and 0.39 mg of excess nitrate per gram of solution. The uranium isotopic content is 92.6 wt % 235U, 5.9 wt % 238U, 1.0 wt % 234U, and 0.5 wt % 236U. The temperature is 293 Kelvin.
SOLUTION MIX=2 RHO[UO2(NO3)2]=415 92235 92.6 92238 5.9 92234 1 92236
0.5 MASSFRAC[HNO3]=6.339-6 TEMPERATURE=293 END SOLUTION
where
The molecular weight of NO3 is 62.0049 g/mole, of H is 1.0078 g/mole, so the grams of excess H per gram of solution is 1.0078 / 62.0049 \(\times\) (0.39 mg/g) \(\times\) (1 g/1000 mg) = 6.339 \(\times\) 10-6.
7.1.4.1.6. Combinations of standard composition materials to define a mixture
Frequently more than one standard composition is required to define a mixture. This section contains such examples.
EXAMPLE 1. Boral from B4C and Aluminum.
Create a mixture 6 that is Boral, 15 wt % B4C and 85 wt % Al, having a density of 2.64 g/cm3. Natural boron is used in the B4C. Note that Example 2 demonstrates the use of the keyword DEN= to enter the density of the mixture and avoid having to look up the theoretical density from the table Isotopes in standard composition library, in the section 7.2.2, and calculate the density multiplier (VF)
B4C 6 0.1571 END
AL 6 0.8305 END
EXAMPLE 2. Boral from B4C and Aluminum.
This is the same problem as Example 1 using a different method of specifying the input data. Create a mixture 6 that is Boral, 15 wt % B4C and 85 wt % Al, having a density of 2.64 g/cm3. Natural boron is used in the B4C.
B4C 6 DEN=2.64 0.15 END
AL 6 DEN=2.64 0.85 END
EXAMPLE 3. Boral from Boron, Carbon, and Aluminum.
If neither Boral nor B4C were available in the Standard Composition Library, Boral could be described as follows:
Create a mixture 2 that is Boral composed of 35 wt % B4C and 65 wt % aluminum with an overall density of 2.64 g/cm3. The boron is natural boron.
vf is the density multiplier. (The density multiplier is the ratio of actual to theoretical density.) From the Standard Composition Library chapter, table Isotopes in standard composition library, the theoretical density of aluminum is 2.702 g/cm3; boron is 2.37 g/cm3; and carbon is 2.1 g/cm3. The density multiplier, vf, for Al is (0.65)(2.64)/2.702 = 0.63509. The isotopic abundances in natural boron are known to have some variability. Here it is assumed that natural boron is 18.4309 wt % 10B at 10.0129 amu and 81.5691 wt % 11B at 11.0096 amu. C is 12.000 amu.
Convert the weight percents to atom percents for the natural boron where w denotes weight fraction, a denotes atom fraction, and M denotes atomic mass:
Solving for \(a_{B10}\) gives:
Therefore the atom percent of 11B is, aB11 = 80.1 a%.
Similarly, the mass of the B4C molecule is
[(0.199 \(\times\) 4 \(\times\) 10.0129) + (0.801 \(\times\) 4 \(\times\) 11.0093) + (12.000)] = 55.24407 amu.
The mass of the boron is (55.24407 - 12.000) = 43.24407 amu.
The vf of boron would be \(\left( \frac{43.24407}{55.24407} \right)\left( \frac{(0.35)(2.64)}{2.37} \right)\) = 0.30519
The vf of C would be
The standard composition input data for the Boral follows:
AL 2 0.63509 END
BORON 2 0.30519 END
C 2 0.09558 END
EXAMPLE 4. Boral from 10B, 11B, Carbon, and Aluminum.
Create a mixture 2 that is Boral composed of 35 wt % B4C and 65 wt % aluminum. The Boral density is 2.64 g/cm3. The boron is natural boron.
vf is the density multiplier. Use 0.63581 for AL and 0.08725 for C as explained in Example 3 above. From the Standard Composition Library chapter, Isotopes in standard composition library table, the theoretical density of 10B is 1.00 g/cm3 and 11B is 1.00 g/cm3. As computed in Example 3, the mass of the B4C molecule is 55.25045 amu, and the boron is 19.764 atom % 10B and 80.236 atom % 11B. The mass of 10B is 10.0129 amu and the 11B is 11.0096. Thus, the vf of 10B is
(7.1.8)\[\left( \frac{(4)(0.199)(10.0129)}{55.24407} \right)\left( \frac{(0.35)(2.64)}{1.0} \right)\ \ =\ \ 0.13331\ .\]The vf of 11B is
(7.1.9)\[\left( \frac{(4)(0.801)(11.0093)}{55.24407} \right)\left( \frac{(0.35)(2.64)}{1.0} \right)\ \ =\ \ 0.58998\ .\]
The standard composition input data for the Boral are given as
AL 2 0.63509 END
B-10 2 0.13331 END
B-11 2 0.58998 END
C 2 0.09558 END
EXAMPLE 5. Specify all of the number densities in a mixture.
Create a mixture 1 that is vermiculite, defined as
hydrogen at a number density of 6.8614-4 atoms/b-cm
oxygen at a number density of 2.0566-3 atoms/b-cm
magnesium at a number density of 3.5780-4 atoms/b-cm
aluminum at a number density of 1.9816-4 atoms/b-cm
silicon at a number density of 4.4580-4 atoms/b-cm
potassium at a number density of 1.0207-4 atoms/b-cm
iron at a number density of 7.7416-5 atoms/b-cm
In this example we use the 2nd syntax option described in Sect. 7.1.3.3, in which the 3rd entry must be 0. The standard composition input data for the vermiculite are given below:
H 1 0 6.8614-4 END O 1 0 2.0566-3 END MG 1 0 3.5780-4 END AL 1 0 1.9816-4 END SI 1 0 4.4580-4 END K 1 0 1.0207-4 END FE 1 0 7.7416-5 END
7.1.4.1.7. Combinations of user-defined compound and user-defined mixture/alloy to define a mixture
Mixtures can usually be created using only basic standard composition specifications. Occasionally, it is convenient to create two or more user-defined materials for a given mixture. This procedure is demonstrated in the following example.
EXAMPLE 1. Specify Boral using a user-defined compound and user-defined mixture/alloy.
Create a mixture 6 that is Boral, 15 wt % B4C and 85 wt % Al, having a density of 2.64 g/cm3. Natural boron is used in the B4C. Boral can be described in several ways. For demonstration purposes, it will be described as a combination of a user-defined compound and user-defined mixture/alloy. This is not necessary, because both B4C and Al are available as standard compositions. A method of describing the Boral without using user-defined compounds or user-defined mixtures/alloys is given in Examples 1 and 2 of Sect. 7.1.4.1.6. The minimum generic input specifications for this user-defined compound and alloy are
ATOM-B4C 6 2.64 2 5000 4 6012 1 0.15 END WTPT-AL 6 2.64 1 13027 100.0 0.85 END
7.1.4.1.8. Combinations of solutions to define a mixture
This section demonstrates the use of more than one solution definition to describe a single mixture. The assumptions used in processing the cross sections are likely to be inadequate for solutions of mixed oxides of uranium and plutonium. Therefore, this section is given purely for demonstration purposes.
EXAMPLE 1. Solution of uranyl nitrate and plutonium nitrate.
Note that the assumptions used in processing the cross sections are likely to only be adequate for CENTRM/PMC calculations of mixed-oxide solutions. This example is given purely for demonstration purposes. Create a mixture 1 consisting of a mixture of plutonium nitrate solution and uranyl nitrate solution. The specific gravity of the mixed solution is 1.4828. The solution contains 325.89 g (U + Pu)/L soln. The acid molarity of the solution is 0.53. In this solution 77.22 wt % of the U+Pu is uranium. The isotopic abundance of the uranium is 0.008% 234U, 0.7% 235U, 0.052% 236U, and 99.24% 238U. The isotopic abundance of the plutonium is 0.028% 238Pu, 91.114% 239Pu, 8.34% 240Pu, 0.426% 241Pu, and 0.092% 242Pu. Note that a single quote in the first column indicates a comment line in SCALE input.
' Uranium density of 77.22% of 325.89 g/L SOLUTION MIX=1 RHO[UO2(NO3)2]=251.65 92234 .008 92235 .700 92236 .052 92238 99.240 ' Plutonium density if 22.78% of 325.89 g/L RHO[PU(NO3)4]=74.24 94238 .028 94239 91.114 94240 8.34 94241 .426 94242 .092 ' Acid molarity is 0.53 M MOLAR[HNO3]=0.53 ' Specifying the density over specifies the problem, which means the solution may ' not be in thermodynamic equilibrium. The specification below adds about 0.3% ' extra hydrogen to the problem DENSITY=1.4828 END SOLUTION
7.1.4.1.9. Combinations of basic and user-defined standard compositions to define a mixture
EXAMPLE 1. Burnable poison from B4C and Al2O3.
Create a mixture 6 that is a burnable poison with a density of 3.7 g/cm3 and composed of Al2O3 and B4C. The material is 1.395 wt % B4C. The boron is natural boron. This material can be easily specified using a combination of user-defined material to describe the Al2O3 and a simple standard composition to define the B4C. The minimum generic input specification for this user-defined material and the standard composition are
The density multiplier of the B4C is the density of the material times the weight percent, divided by the theoretical density of B4C [(3.7 \(\times\) 0.01395)/2.52] or 0.02048; the density multiplier of the Al2O3 is 1.0 - 0.01395 or 0.98605 (the theoretical density of B4C was obtained from Isotopes in standard composition library table in the STDCMP chapter).
The input data for the burnable poison are given below:
ATOM-AL2O3 6 3.70 2 13027 2 8016 3 0.98605 END B4C 6 2.048-2 ENDThe B4C input can be specified using the DEN= parameter as shown below:
ATOM-AL2O3 6 3.70 2 13027 2 8016 3 0.98605 END B4C 6 DEN=3.7 0.01395 ENDThe fraction of B4C in the mixture is ((3.7 \(\times\) 0.01395)/2.52) = 0.02048. The fraction of Al2O3 in the mixture is 1.0 - 0.02048 = 0.979518. The density of the Al2O3 can be calculated as shown below.
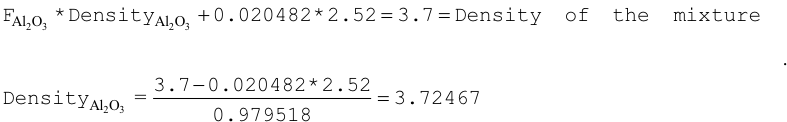
Input data using the density of Al2O3 are given below:
ATOM-AL2O3 6 3.72467 2 13027 2 8016 3 END B4C 6 2.048-2 END
EXAMPLE 2. Borated water from H3BO3 and water.
Create a mixture 2 that is borated water at 4350 parts per million (ppm) by weight, resulting from the addition of boric acid, H3BO3 to water. The density of the borated water is 1.0078 g/cm3 (see “Specific Gravity of Boric Acid Solutions,” Handbook of Chemistry, 1162, Compiled and Edited by Norbert A. Lange, Ph.D, 1956.). The solution temperature is 15ºC and the boron is natural boron.
An easy way to describe this mixture is to use a combination of a user-defined compound to describe the boric acid, and a basic composition to describe the water.
STEP 1. INPUT DATA TO DESCRIBE THE USER-DEFINED COMPOUNDThe generic input data for the boric acid are given below. The actual input data are derived in steps 2 through 5.
ATOMH3BO3 2 0.025066 3 5000 1 1001 3 8016 3 1.0 288.15 END
STEP 2. AUXILIARY CALCULATIONS FOR THE USER-DEFINED COMPOUND INPUT DATA
In calculating the molecular weights, use the atomic weights from SCALE, which are available in the table Isotopes in standard composition library in Sect. 7.2.2 of the SCALE manual. The atomic weights used in SCALE may differ from some periodic tables. The SCALE atomic weights used in this problem are listed below:
H (1001) 1.0078
O (8016) 15.9949
10B 10.0129
11B 11.0093
The natural boron abundance, in weight percent, is defined to be:
10B 18.4309
11B 81.5691
The molecular weight of natural boron is given by
DEN nat B/AWT nat B = DEN 10B/AWT 10B + DEN 11B/AWT 11B
DEN 10B = WTF 10B \(\times\) DEN nat B
DEN 11B = WTF 11B \(\times\) DEN nat B
where:
DEN is density in g/cm3,
AWT is the atomic weight in g/mol,
WTF is the weight fraction of the isotope.
Substituting,
DEN nat B/AWT nat B = DEN nat B \(\times\) ((WTF 10B/AWT 10B) + (WTF 11B/AWT 11B))
Solving for AWT nat B yields:
AWT nat B = 1/((WTF 10B/AWT 10B) + (WTF 11B/AWT 11B))
The atomic weight of natural boron is thus
1.0/((0.184309 g 10B/g nat B/10.0129 g 10B/mol 10B) + (0.815691 g 11B/g nat B/11.0093 g /mol 11B)) = 10.81103 g nat B/mol nat B
The molecular weight of the boric acid, H3BO3 is given by:
(3 \(\times\) 1.0078) + 10.81103 + (3 \(\times\) 15.9949) = 61.8191
Calculate the grams of boric acid in a gram of solution:
Boric acid, H3BO3 is 61.8222 g/mol
Natural boron is 10.81261 g/mol
(4350 \(\times\) 10-6 g B/g soln) \(\times\) (1 mol/10.81261 g B) \(\times\) (61.8191 g boric acid/mol) =
0.024874 g boric acid/g soln (2.4874 wt %)
Interpolating from the referenced page from Lange’s Handbook of Chemistry, the specific gravity of the boric acid solution at 2.4872 weight percent is 1.0087. This value is based on water at 15\(^{\circ}\). Therefore, the density of the boric acid solution is 1.0087 \(\times\) 0.99913 g/cm3 = 1.0078 g soln/cm3.
Calculate ROTH, the theoretical density of the boric acid.
1.0078 g soln/cm3 \(\times\) 0.024874 g boric acid/g soln = 0.025068 g boric acid/cm3
STEP 3. DESCRIBE THE BASIC STANDARD COMPOSITION INPUT DATA
H2O 2 0.984507 288.15 END
where the volume fraction =0.984506 (see step 4 auxiliary calculations below)
STEP 4. AUXILIARY CALCULATIONS FOR THE BASIC STANDARD COMPOSITION INPUT DATA
Calculate the volume fraction of the water in the solution, assuming 0.9982 is the theoretical density of water from Table 7.2.4. Each gram of solution contains 0.024872 g of boric acid, so there is 0.975128 g of water in each gram of solution. The volume fraction of water is then given by:
(1.0078 g soln/cm3 \(\times\) 0.975128 g water/g soln)/0.9982 g water/cm3 = 0.984506
STEP 5. CREATE THE MIXTURE FOR BORATED WATER
ATOMH3BO3 2 0.025068 3 5000 1 1001 3 8016 3 1.0 288.15 END
H2O 2 0.984506 288.15 END
7.1.4.1.10. Combinations of basic and solution standard compositions to define a mixture
The solution specification is the easiest way of specifying the solutions listed in the Available fissile solution components table in Sect. 7.2.3. A combination of solution and basic standard compositions can be used to describe a mixture that contains more than just a solution as demonstrated in the following example.
EXAMPLE 1. Uranyl nitrate solution containing gadolinium.
Create a 4.306% enriched uranyl nitrate solution containing 0.184 g gadolinium per liter. The uranium in the nitrate is 95.65% 238U, 0.022% 236U, 4.306% 235U, and 0.022% 234U. The uranium concentration is 195.8 g U/L and the specific gravity of the uranyl nitrate is 1.254. There is no excess acid in the solution. The presence of the gadolinium is assumed to produce no significant change in the solution density. The solution is defined to be mixture 3.
SOLUTION MIX=3
RHO[UO2(NO3)2]=195.8 92238 95.65 92236 0.022 92235 4.306 92234 0.022
VOL_FRAC=0.99985
DENSITY=1.254
END SOLUTION
GD 3 0.000184 293 END
7.1.4.1.11. Combinations of user-defined compound and solution to define a mixture
The solution specification is the easiest way of specifying the solutions listed in the Available fissile solution components table in Sect. 7.2.3 of the SCALE manual. A solution specification and user-defined compound specification can be used to describe a mixture that contains more than just a solution as demonstrated in the following example.
EXAMPLE 1. Uranyl nitrate solution with gadolinium nitrate.
Create a 4.306% enriched uranyl nitrate solution containing gadolinium in the form of Gd(NO3)3. The uranium in the nitrate is 95.65% 238U, 0.022% 236U, 4.306% 235U, and 0.022% 234U. The uranium concentration is 195.8 g U/L and the density of the uranyl nitrate is 1.254. There is no excess acid in the solution. The concentration of the gadolinium is 0.184 g/L. The volume fraction of the mixture that is uranyl nitrate (0.99985 = 1.254/ (1.254 + 0.000184)). The solution is defined to be mixture 3.
SOLUTION MIX=3
RHO[UO2(NO3)2]=195.8 92238 95.65 92236 0.022 92235 4.306 92234 0.022
VOL_FRAC=0.99985
DENSITY=1.254
END SOLUTION
The density of the gadolinium is given as 0.184 g/L. To describe the user-defined compound, the density of the Gd(NO3)3 is needed. The atomic weights from the Standard Composition Library are:
Gd 157.25
N 14.0067
O 15.999
Therefore, the density of the Gd(NO3)3 = 0.000184 g Gd/cm3 \(\times\) (157.25 + 3(14.0067 + 3(15.999))/157.25) = 0.0004017 g/cm3.
The input data for this user-defined compound are given below:
ATOMGD(NO3)3 3 .0004017 3 64000 1 7014 3 8016 9 1.0 300 END
The complete input data for the mixture of uranyl nitrate and gadolinium nitrate are given as:
SOLUTION MIX=3
RHO[UO2(NO3)2]=195.8 92238 95.65 92236 0.022 92235 4.306 92234 0.022
VOL_FRAC=0.99985
DENSITY=1.254
END SOLUTION
ATOMGD(NO3)3 3 .0004017 3 64000 1 7014 3 8016 9 1.0 300 END
Note
Since the default temperature (300 K) is to be used, it can be omitted from the user-defined compound standard composition. The temperature must be entered if the standard composition contains a multiple-isotope nuclide whose isotopic abundance is to be specified.