9.1. XSDRNPM: A One-Dimensional Discrete-Ordinates Code for Transport Analysis
L. M. Petrie, N. M. Greene, M. L. Williams
ABSTRACT
XSDRNPM is a discrete-ordinates code that solves the one-dimensional Boltzmann equation in slab, cylindrical, or spherical coordinates. Alternatively, the user can select P1 diffusion theory, infinite medium theory, or Bn theory. A variety of calculational types is available, including fixed source, eigenvalue, or “search” calculations. In SCALE, XSDRNPM is used for several purposes: eigenvalue (k-effective) determination, cross-section collapsing, shielding analysis, computation of fundamental-mode or generalized adjoint functions for sensitivity analysis, and for producing bias factors for use in Monte Carlo shielding calculations.
ACKNOWLEDGMENTS
W. W. Engle has been very generous with the use of his notes on \(S_n\) theory and on discussing details of various procedures in XSDRNPM which were lifted directly from his ANISN program.
The authors also wish to thank R. H. Odegaarden (the former technical monitor at the U.S. Nuclear Regulatory Commission) who supplied the necessary incentives for completing this report.
9.1.1. Introduction
XSDRNPM is a one-dimensional (1-D) discrete-ordinates transport code and is the latest in a series of codes in the XSDRN [XSDGCJ69] family. As such, it contains several unique characteristics, as will be detailed in this report, though a large portion of the theoretical bases and intended uses of the program are the same for all versions.
9.1.1.1. Functions performed
The function of XSDRNPM is twofold: (1) perform a 1-D discrete-ordinates calculation in slab, cylindrical, or spherical geometry (optionally, a 1-D diffusion theory or infinite medium |Bn| calculation can be made), and (2) use the fluxes determined from its spectral calculation to collapse input cross sections and write these into one of several formats.
A great deal of flexibility is allowed in describing a problem for XSDRNPM. The number of spatial intervals, the number of energy groups, the number of nuclides, the quadrature order, the order of fits to the angular variation in basic cross sections are all arbitrary and are limited only by computer and monetary resources.
The flux calculation can be performed according to several options, including fixed source calculations, k-calculations, and dimension search calculations.
A variety of weighting options are allowed, including zone, cell, or a special “vein” weighting option which is described herein.
9.1.1.1.1. Background on XSDRNPM
Development of the XSDRN1 program started in the mid-1960s. The goal was to develop a program that would combine features from the GAM-II, [XSDJD63] ANISN, [XSDEJ67] and THERMOS [XSDHon61] programs in a more unified and general way than would be possible if one simply elected to use these codes individually.
The salient features to be retained from the programs were as follows:
- GAM-II
The Nordheim Integral Treatment was desired for resonance self-shielding; the generality of including cross sections for an arbitrary number of processes, along with the provisions for truncating zero or impossible transfers in the scattering matrices, was also a requirement.
- ANISN
One-dimensional discrete-ordinates or diffusion theory or infinite-medium theory was to be available to generate a spectrum for cross-section collapsing.
- THERMOS
The ability to perform detailed 1-D spectral calculations, including upscatter effects, was required for the thermal region.
The whole code was required to be dynamically dimensioned to allow calculations for arbitrary group structures, spatial structures, angular quadratures, etc.
The XSDRN program that embodied these features was released in 1969.
In the early 1970s, the Defense Nuclear Agency (DNA) initiated support for the AMPX system, which was to be a total cross-section generation system capable of performing all tasks necessary to take basic neutron and gamma-ray cross-section data and process these data into the proper form needed for weapons effects calculations. Since XSDRN already encompassed many of the features needed, it was selected as a basis for modules in the new system. In this case, experience gained in the original construction of XSDRN served to suggest that a more modular approach would have been better with independent tasks being done in separate, smaller, easier-to-manage programs. Therefore, the code was split into NITAWL-II (for resonance self-shielding and some basic cross-section data manipulation) and XSDRNPM (for spectral calculations and cross-section collapsing). In retrospect, if the AMPX development were initiated today, XSDRN would have been split even further, into perhaps as many as six or seven programs.
The XSDRNPM module differs from XSDRN in several respects:
It will perform coupled neutron-gamma calculations.
It allows any mixture to be represented to an arbitrary order of anisotropic representation, whereas XSDRN only allowed through order 3.
It will perform an adjoint calculation, whereas the option was never provided in XSDRN. In 2010, a generalized adjoint solution was also added.
It is considerably more efficient in the manner in which data storage is used and, hence, will run much larger problems in less core storage.
It employs improved thermal flux scaling techniques for better problem convergence.
Input specifications have been reordered, and more defaults have been provided to make the use of this module easier.
It will calculate \(S_n\) constants for any order for any of the three 1-D geometries available.
Mixture-dependent fission spectra are calculated and used in XSDRNPM, which takes into account all fissionable nuclides in a problem.
AMPX was released in 1976, about the same time as the U.S. Nuclear Regulatory Commission (NRC) support for the SCALE system was initiated. Although separate versions of XSDRNPM were initially maintained for AMPX and SCALE, in recent years the same version is used for the two systems.
9.1.1.2. Applications in SCALE
XSDRNPM is used in several places in SCALE. In SAS1, XSDOSE uses fluxes from a 1-D shielding calculation to determine a dose rate. Within the CSAS5 and CSAS6 control modules, XSDRNPM is used in the sequences to perform eigenvalue calculations and cell weighting of cross sections. TSUNAMI-1D uses XSDRN to compute forward and adjoint fluxes (fundamental-mode and generalized adjoint) for sensitivity and uncertainty analysis.
9.1.1.2.1. Notes on the use of various spectral calculational options
As noted earlier, four options are available in XSDRNPM for calculating fluxes, k-effectives, etc.:
\(S_n\) theory,
diffusion theory,
infinite medium theory, and
\(B_n\) theory.
However, XSDRNPM is primarily an \(S_n\) code. The latter three options are provided for reasons of completeness and are not nearly as optimized as they would be in other codes for which these are the primary spectral calculation options.
Without a very detailed calculational study, it is perhaps impossible to be able to quantify the degree of adequacy or inadequacy of any of these methods for performing a particular problem. However, some general comments can be made which may provide some guidance with their selection.
First, \(S_n\) theory is the most correct of the options and will solve a larger class of problems. It is the most complicated and time-consuming of the four, but it still runs very fast for most cases. There are problems for which it (or some alternative method based on a solution of the Boltzmann equation) is the only one of the four methods which is adequate. Many shielding applications fall in this class. In deep-penetration problems, anisotropic effects can dominate, thus requiring an accurate treatment of the anisotropy of both flux and cross section. It is well known that diffusion theory is not very accurate when used to calculate systems involving regions of very dissimilar cross-section values, such as is the case when control rods are interspersed in a reactor core. Because of the anisotropy involved in gamma-ray problems, \(S_n\) theory should be used.
Diffusion theory, on the other hand, is certainly the most successful of the four methods in terms of the amount of use it has for designing reactors, etc. In cases involving reasonably large, homogeneous regions, it is generally adequate, such as is the case for a large class of “reactor” applications. For most problems, the diffusion theory option should run appreciably faster than \(S_n\) theory, since it has essentially one equation to solve, versus number-of-angles equations for \(S_n\) theory. This equation also can be explicitly solved using a matrix inversion procedure, whereas the \(S_n\) theory requires a more time-consuming iterative procedure. However, in many cases with large numbers of groups (200 to 300), the greater fraction of the calculational time can be spent calculating the scattering source terms, which tends to lessen the impact of time spent on a more correct theory. (This same observation can also be made of the infinite medium and \(B_n\) method.)
The infinite medium option is the fastest of the four methods and can be used safely to perform calculations for large homogeneous regions, wherein the spectrum may be needed to collapse cross sections. This option only determines the first moment of the flux, and is, therefore, quite suspect for many applications, such as calculating diffusion coefficients.
The \(B_n\) option shares many of the same restrictions as the infinite-medium method; however, this treatment does (as its name implies) use a buckling approximation to account for leakage from the large homogeneous region, thereby giving higher order flux moments that can be used, for example, to determine diffusion coefficients.
9.1.1.3. Selection of output cross-section library formats
XSDRNPM will, on option, collapse cross sections and write the collapsed sets into four different formats:
ANISN3 BCD Library,
ANISN3 Binary Library,
CCCC [XSDCar74] ISOTXS Library, or
AMPX [XSDWWCD15] Working Library.
The choice of the output cross-section format is determined by the computer code that will use the data. XSDRNPM always produces an AMPX working library when cross sections are collapsed, and all other formats are produced by reformatting data from this library. Therefore, for archival purposes, if a collapsed library is to be saved, the working format is the best choice, because it is the most general of those provided. AMPX working libraries are used by all multi-group transport codes currently in SCALE, including DENOVO (3D orthogonal mesh discrete ordinates code), NEWT (2D arbitrary mesh discrete ordinates code), and KENO and MONOCO (multigroup Monte Carlo codes. Stand-alone modules exist for converting AMPX working libraries to the other formats.
ANISN formats are used by older ORNL transport codes such as ANISN (a 1-D discrete-ordinates code), by DORT/TORT [XSDRSCEJ79] [two-dimensional (2-D) and three dimensional (3D) discrete-ordinates codes], and by MORSE [XSDEme75] (a multigroup Monte Carlo code). The formats are quite comprehensive and can handle coupled neutron-gamma calculations, arbitrary orders of anisotropy, upscattering, etc. The major shortcoming of the format is its lack of internal documentation as to its structure (e.g., no provisions exist for specifying where a particular kind of cross section is located in the library or even if it is included). ANISN libraries can be produced in a free-form card-image BCD format or in a binary form.
The CCCC (Committee on Computer Code Coordination) ISOTXS file is a format for neutron cross sections that is one of several “standard interfaces” developed to facilitate the exchange of data between different computer codes. It is a self-defined format, which has provisions for identifying cross sections in the library. Scattering matrices can be supplied for elastic, inelastic, and (n,2n) scattering.
9.1.2. Theory and Procedures
This section describes the models and procedures which are employed in XSDRNPM.
9.1.2.1. One-dimensional discrete-ordinates theory
The time-independent Boltzmann transport equation can be written:
This expression is a balance condition that states simply that losses due to leakage (first term) and collisions (second term) must equal the source of neutrons, at some point in space \(r\) energy E, and in direction \(\Omega\) per unit volume and energy and solid angle. Other terms in the expression are \(\sum_{t}(r, E)\) the total macroscopic cross section of the medium, which is typically assumed isotropic, and the flux, \(\psi(r, E, \Omega)\).
The source term \(S(r, E, \Omega)\) has three components:
a scattering source, \(S(r, E, \Omega)\),
a fission source, \(F(r, E, \Omega)\), and
a fixed source, \(Q(r, E, \Omega)\).
The scattering source is given by:
The fission source term, typically, is written
where \(\sum_{s}\left(r, E^{\prime} \rightarrow E, \Omega^{\prime} \rightarrow \Omega\right)\) is the macroscopic scattering cross section per unit energy for scattering from energy E’ to E, \(\chi(r, E)\) is the fraction of the fission neutrons per unit energy produced at r and E, \(\upsilon(r, E)\) is the average number of neutrons produced per fission, \(\sum_{f}(r, E)\) is the macroscopic fission cross section and k is the “effective multiplication constant.” Note that, as in the case of the total cross-section value, \(\chi\),\(\Sigma\)f, and \(\upsilon\) are assumed to be isotropic. XSDRN computes a weighted-averaged fission spectrum based on the fissionable materials at r.
Three common coordinate systems are shown in Fig. 9.1.1. XSDRNPM is a 1-D code, which means that in the case of the slab, it is calculating at points along one axis where the system is assumed to extend to infinity along the other two axes. If we assume a calculation along the x-axis, this says that there is no leakage in the y or z directions, and our directions by angles referenced to the x-axis. In the case of the cylinder, the length (z-axis) is infinite and the calculation is for points (shells) located at distance r from the central axis. For the sphere, the calculation is of shells located at radius, r, from the center of the spherical system.
Fig. 9.1.2 illustrates the 1-D coordinate systems for slabs, cylinders, and spheres. Note that the directions are cones in the case of the slab and sphere, whereas in the case of the cylinder, the same simple symmetries do not hold (a cone around the radius does not strike the next cylindrical shell at the same distance from a point on a radius) and the directions must be specifically described. Symmetries in the 1-D cylinder, however, allow one to only describe directions for one quadrant of the direction sphere about a point as will be noted in Sect. 9.1.2.2.
The 1-D geometries allow considerable simplification to be made to Eq. Eq. (9.1.1), especially in the leakage term \(\bar{\Omega} \bullet \nabla \psi\). It is traditional to calculate the angular flux as a function of angles expressed in direction-cosine units; i.e., \(\mu=\cos \phi\) and \(\eta=\cos \xi\). This requires \(\psi(x, E, \mu)\) for slabs, \(\psi(x, E, \mu, \eta)\) for cylinders and \(\psi(r, E, \mu)\) for spheres. Table 9.1.1 gives leakage terms expressed in conservation form for the three geometries.
Geometry |
\(\overset{\rightharpoonup}{\Omega} \bullet \nabla \psi\) |
Slab |
\(\mu \frac{\partial \psi}{\partial x}\) |
Cylinder |
\(\frac{\mu}{r} \frac{\partial(r \psi)}{\partial r}-\frac{1}{r} \frac{\partial(\eta \psi)}{\partial \phi}\) |
Sphere |
\(\frac{\mu}{r^{2}} \frac{\partial\left(r^{2} \psi\right)}{\partial r}+\frac{1}{r} \frac{\partial\left[\left(1-\mu^{2}\right) \psi\right]}{\partial \mu}\) |
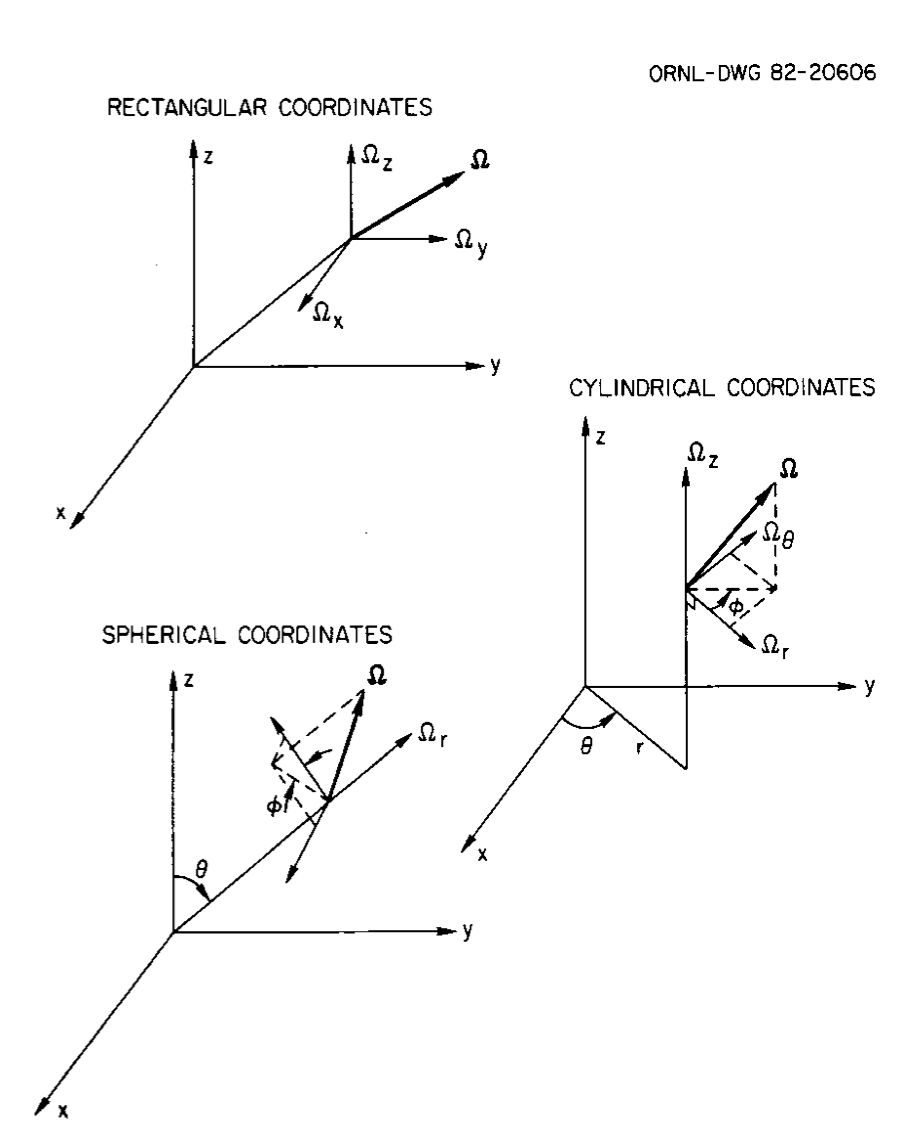
Fig. 9.1.1 Three common coordinate systems.
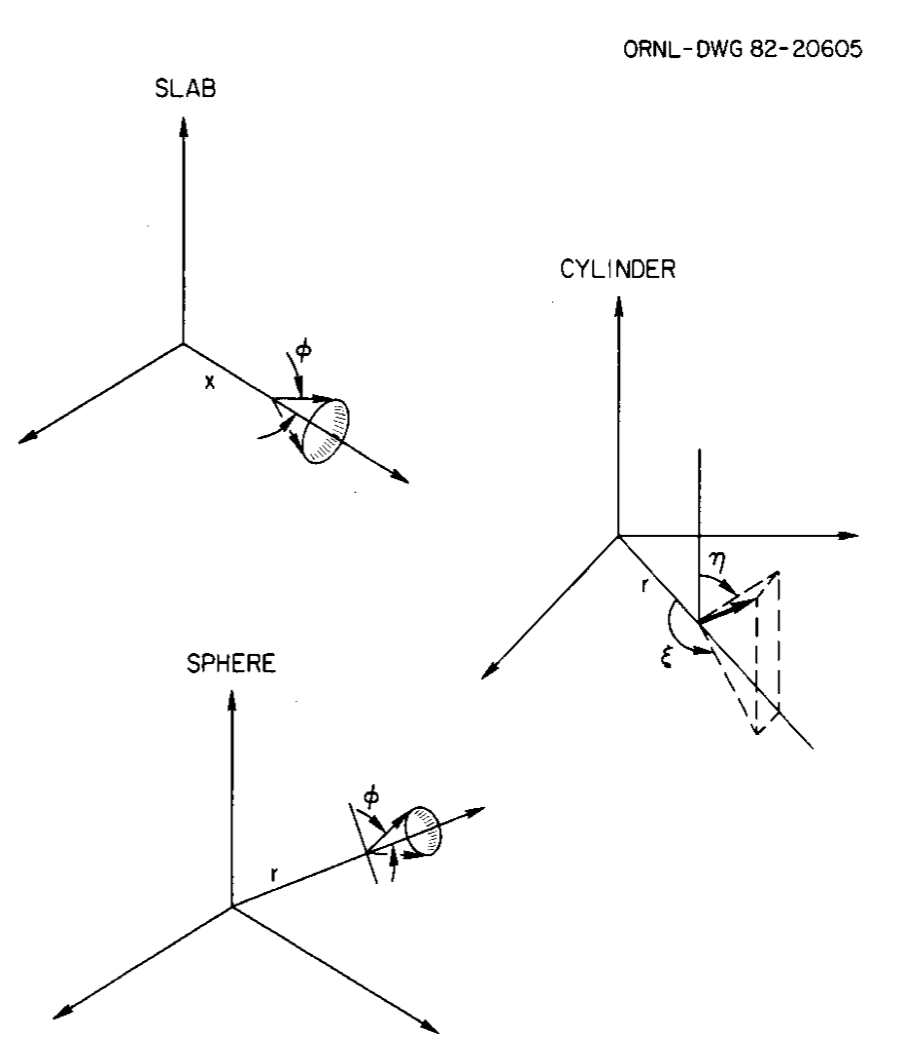
Fig. 9.1.2 Three 1-D coordinate systems.
9.1.2.2. Multigroup one-dimensional Boltzmann equation
In multigroup schemes, the continuous-energy (CE) balance equations are converted to multigroup form by first selecting an energy structure and then writing a multigroup equivalent of the point equation which requires multigroup constants that tend to preserve the reaction rates that would arise from integrating the CE equations by group. First we define the following multigroup values for g,
and
and
where W(x.E) is the weighting function used to compute the multigroup cross sections at a particular location. To rigorously conserve reaction rates, the weight function should be angle-dependent, but this causes the multigroup cross section to vary with direction; therefore the usual approach is to represent the weight function by an approximation to the scalar flux spectrum. In energy ranges where the CE cross sections have fine-structure due to resonances, the multigroup data must be self-shielded prior to the multigroup transport calculations.
The following multi-group form of 1-D equation can be derived for the slab case:
The equations for the cylinder and sphere are essentially the same, in this notation, except for the differences in the leakage terms from Table 9.1.1.
In Eq. Eq. (9.1.7) , Sg, Fg, and Qg are the scattering, fission, and fixed sources, respectively. The scattering term is discussed in Sect. 9.1.2.3. The multigroup form of the fission source is
where \(\chi_g\) is the fraction of the fission neutrons that are produced in group g, and \(\overline{v \Sigma_{f{g}^{\prime}}}\) is the average of the product of \(\nu\), the average number of neutrons produced per fission and \(\Sigma_f\), the fission cross section.
9.1.2.3. Scattering source term
In discrete-ordinates theory, one typically calculates the Legendre moments of the flux, \(\psi_{g,l}\), defined for slab and spherical geometries by
Cylindrical geometry has a similar expression containing spherical harmonic functions rather than Legendre polynomials, shown in the next section.
The group-to-group scattering coefficients are, themselves, fit with Legendre polynomials, such that
In this example, we have a fit of order ISCT.
Note
AMPX cross-section libraries contain the 2l + 1 factor in the \(\sigma_{t}\left(g^{\prime} \rightarrow g\right)\) matrix.
9.1.2.3.1. Slab and Spherical Geometries
Because of the symmetries in 1-D slabs and spheres, only one angle is needed to describe a “direction.” In the case of the slab, the angle is taken with reference to the x-axis, while for the sphere; it is with reference to a radius vector between the point and the center of the sphere. This means that the flux can be expanded in ordinary Legendre polynomials, such that
When Eq. Eq. (9.1.11) and Eq. Eq. (9.1.10) are introduced into Eq. Eq. (9.1.2), the following expression is derived for the scattering source:
where ISCT is the order of fit to the fluxes and cross sections.
9.1.2.3.2. Cylindrical Geometry
The situation is more complicated in the case of the 1-D cylinder where the flux (and cross section) must be given as a function of two angles. Consider Fig. 9.1.3.
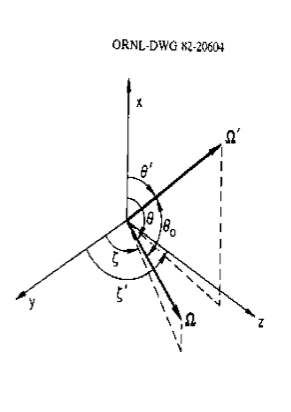
Fig. 9.1.3 One-dimensional cylindrical scattering coordinates.
The addition theorem for associated Legendre polynomials can be used to transform from scattering angle coordinates to the real coordinates required in the cylindrical case:
where \(\mu_{0}=\cos \theta_{0}\); \(\mu=\cos \theta\) and \(\mu^{\prime}=\cos \theta^{\prime}\).
If we note that
Eq. Eq. (9.1.13) can be introduced into Eq. Eq. (9.1.2) to yield
Now it is convenient to recall that
which can be introduced into Eq. Eq. (9.1.15) and rearranged to give
We now define moments of the flux, \(\psi_{l}\) by
It is also convenient to make use of the trigonometric relationship
and
With a 1-D cylinder, the flux is symmetric in \(\zeta\); therefore, it is an even function, and the terms involving sin n \(\zeta\) will vanish. This fact yields the following expression for Eq. Eq. (9.1.17) :
We observe further that for an even function in \(\zeta\), the odd l and odd (l-n) moments must all vanish, such that the following moments are nonzero for various orders of scattering:
ISCT |
Nonzero flux moments |
|---|---|
0 |
\(\psi_{0}\) |
1 |
\(\psi_{0}\), \(\psi_{1}^{1}\) |
2 |
\(\psi_{0}, \psi_{1}^{1}, \psi_{2}, \psi_{2}^{2}\) |
3 |
\(\psi_{0}, \psi_{1}^{1}, \psi_{2}, \psi_{2}^{2}, \psi_{3}^{1}, \psi_{3}^{3}\) |
4 |
\(\psi_{0}, \psi_{1}^{1}, \psi_{2}, \psi_{2}^{2}, \psi_{3}^{1}, \psi_{3}^{3}, \psi_{4}, \psi_{4}^{2}, \psi_{4}^{4}\) |
In general, [ISCT(ISCT + 4)/4] + 1 flux moments are required.
9.1.2.4. Discrete-ordinates difference equations
In formulating the \(S_n\) equations, several symbols are defined which relate to a flux in an energy group g, in a spatial interval i, and in an angle m.
Typically, the flux is quoted as an integral of the flux in an energy group g, whose upper and lower bounds are \(E_{g}^{U}\) and \(E_{g}^{L}\) respectively.
A mechanical quadrature is taken in space, typically IM intervals with IM + 1 boundaries. Likewise, an angular quadrature is picked compatible with the particular 1-D geometry, typically MM angles with associated directional coordinates and integration weights.
The different equations are formulated in a manner which involves calculating so-called angular fluxes, \(\psi_{g,i,m}\) at each of the spatial interval boundaries, and also cell-centered fluxes, \(\psi_{g, i+1 / 2, m}\) at the centers of the spatial intervals. The centered fluxes are related to the angular boundary fluxes by “weighted diamond difference” assumptions as will be described below.
Units on angular fluxes are per unit solid angle wm and per unit area. Units on the centered fluxes are track length per unit volume of the interval. In both cases the fluxes are integrated in energy over the group g.
The areas and volumes for the three geometries are listed in Table 9.1.2
Geometry |
Area |
Volume |
|---|---|---|
Slab |
1.0 |
\(x_{i+1}-x_{i}\) |
Cylinder |
\(2 \pi r_{i}\) |
\(\pi \left(r_{i+1}^{2}-r_{i}^{2}\right)\) |
Sphere |
\(4 \pi r^{2}\) |
\(4/3 \pi \left(r_{i+1}^{3}-r_{i}^{3}\right)\) |
9.1.2.4.1. Discrete-ordinates equation for a slab
Consider a spatial cell bounded by \(\left( x_i,x_{i+1}\right)\) and write the loss term for flow through the cell in direction \(\mu_m\). The net flow in the x-direction out the right side is the product of the angular flux times the area times the solid angle times the cosine of the angle:
The net loss from the cell is the difference between the flow over both boundaries:
The loss in the spatial cell due to collisions is given by the product of the centered angular flux (in per unit volume units) times the total macroscopic cross section times the solid angle times the volume:
The sources in direction \(\mu_m\) are given by the product of the solid angle times the interval volume times the volume-averaged source (sum of fixed, fission, and scattering) in the direction m:
The slab equation is obtained by using Eqs. Eq. (9.1.24), Eq. (9.1.25), and Eq. (9.1.26) and substituting proper values for area and volume:
In an MM angle quadrature set, there are MM of these equations and they are coupled through the assumption on how the cell-centered flux relates to the boundary angular fluxes, the sources, and the boundary conditions, as will be discussed later.
9.1.2.4.2. Discrete-ordinates equations for sphere and cylinder
The development of the equations for these geometries is analogous to that for the slab except that the leakage terms are more complicated. Consider Fig. 9.1.4.
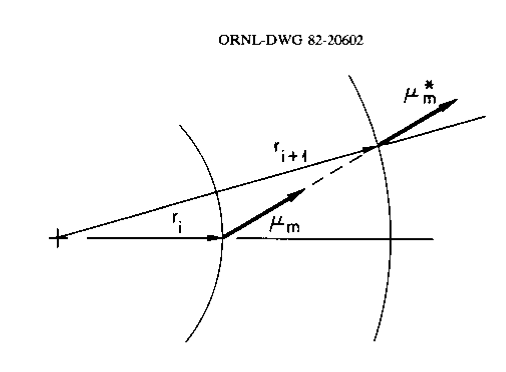
Fig. 9.1.4 Angular redistribution in spherical geometry.
Recall that the directions are taken with reference to the radius vector for a sphere. A particle traveling in direction \(\mu_m\) at \(r_i\) will intersect the radius vector to the next point \(r_{i+1}\) at a different angle \(\mu_{m}^{*}\). The same effect also exists for the cylinder, though in this case the direction coordinates are more complicated. Because of the effect, a loss term is included for the “angular redistribution.” It is defined in a manner analogous to Eq. Eq. (9.1.24) as
where the \(\alpha\) coefficients are to be defined in such a manner as to preserve particle balance. In this case one speaks of \(m + 1\) and \(m-1 / 2\) as the corresponding angles to \(\mu_m\) on the I + lth and ith boundaries, respectively. (See Fig. 9.1.5) Here we are interested in an angle \(\mu_m\) at the center of interval i which redistributes to \(\mu_{m-\frac{1}{2}}\) at boundary i and to \(\mu_{m+\frac{1}{2}}\) at boundary I + 1.
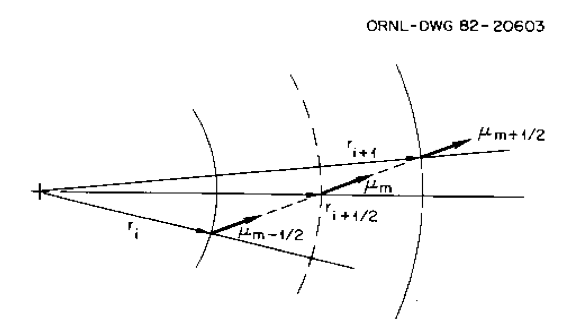
Fig. 9.1.5 Angular redistribution.
Obviously, it is necessary that the net effect of all redistributing be zero, in order to maintain particle balance. This condition is met if
where we have dropped the group and interval indexes.
In order to develop an expression for determining the \(\alpha\)’s consider an infinite medium with a constant isotropic flux. In this case, there is no leakage and the transport equation reduces to
This condition requires that
which when we note that all the \(\psi\) terms in the infinite medium case are equal becomes
which is a recursion relationship for \(\alpha\).
From Eq. Eq. (9.1.29) we see that the conservation requirement can be met if
for any values of flux, and is, therefore, used to evaluate the \(\alpha\)’s along with Eq. eq:eq9-1-27 or eq:eq9-1-28. (Note that had we included the redistribution term in the slab equation, Eq. eq:eq9-1-28 would have given zeroes for the terms, which is as one would expect for this geometry.)
The final discrete-ordinates expression for spheres and cylinders is then derived by summing expressions Eqs. eq:eq9-1-20, eq:eq9-1-24, eq:eq9-1-21 and setting it equal to expression Eq. eq:eq9-1-22.
9.1.2.4.3. \(S_n\) quadratures for slabs
XSDRNPM will automatically calculate quadrature sets for each of the 1-D geometries, or a user can, if he wants, input a quadrature.
In the case of the 1-D slab, the quadrature is a double Gauss-Legendre set based on recommendations from [XSDCL65].
The ordering of the directions for a slab is shown in Fig. 9.1.6.
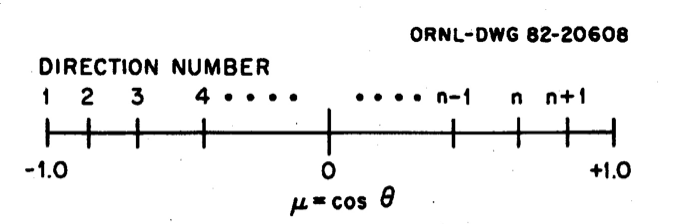
Fig. 9.1.6 Ordering of \(S_n\) directions for slabs and spheres.
Note that in referring to the quadratures for any of the geometries, we do not attempt to define an explicit area on a unit sphere, but rather speak of characteristic directions with associated weights. In the case of the slab, it is convenient to think of “directions” which are shaped like cones, because of the azimuthal symmetry around the x-axis.
In an nth order quadrature, there are n +1 angles with the first angle being taken at \(\mu = -1.0\). This first angle is not required for the slab, but is needed for the curvilinear geometries because of the angular redistribution terms, as will be noted later. It is included in the slab case for reasons of uniformity of programming, etc.
Several requirements are made regarding the angles and weights in the quadrature set.
The arguments relating to angular redistribution can be expected to show that
This situation is ensured if the weight of the \(\mu = -1.0\) direction is zero and the other directions and weights are symmetric about \(\mu = 0\). (The \(\mu = 0\) direction is never included in the quadrature set because of its singularity.)
Further, it is required that
Due to the above normalization of the quadrature weights, the discrete ordinates angular flux is not “per steradian” but rather “per direction-weight”. The calculated angular flux can be converted to steradians by dividing by \(4\pi\).
9.1.2.4.4. \(S_n\) quadratures for spheres
The quadratures generated for spheres are Gauss-Legendre coefficients as recommended by [XSDEme75].
The ordering and symmetry requirements for spheres are the same as for slabs.
In the case of the sphere, the initial (\(\mu = -1.0\)) direction is required, because the difference equations involve three unknown values for each direction, \(\mu_{m}:\psi_m\) and the fluxes at the two “redistributed” angles \(\psi_{m-\frac{1}{2}}\) and \(\psi_{m+\frac{1}{2}}\). It is obvious that an angle along the radius will not involve the redistribution; hence, the expression for this direction involves only \(\psi\left( \mu=-1.0 \right)\) as unknowns. Angle 2 proceeds by assuming \(\psi_{2-\frac{1}{2}}\) is given by \(\psi_1\) and also uses a weighted diamond difference model to relate \(\psi_m\), \(\psi_{m-\frac{1}{2}}\), \(\psi_{m+\frac{1}{2}}\), as will be described below. Subsequent angles will then have values for \(\psi_{m-\frac{1}{2}}\) calculated by the previous angle equations.
9.1.2.4.5. \(S_n\) quadratures for cylinders
The quadrature sets for cylinders are more complicated (see Fig. 9.1.2) because the directions must be specified with two angles, \(\xi\) and \(\eta\) where \(\alpha = \sin \eta \cos \xi\) and \(\beta = \cos \eta\).
In this case, practice is to use n/2 levels of directions for an nth order set. The levels correspond to fixed values of \(eta\). The number of angles by level starts with three in level 1, five in level 2, seven in level 3, etc. (Note that since cylindrical geometry is curvilinear, each level will start with a \(\eta=\pi\) direction that has zero weight for reasons analogous to those given for the spherical case. Fig. 9.1.7 shows the ordering of the directions for an S6 quadrature set. Angles 1, 4, and 9 are the starting directions (zero weight) for the levels.
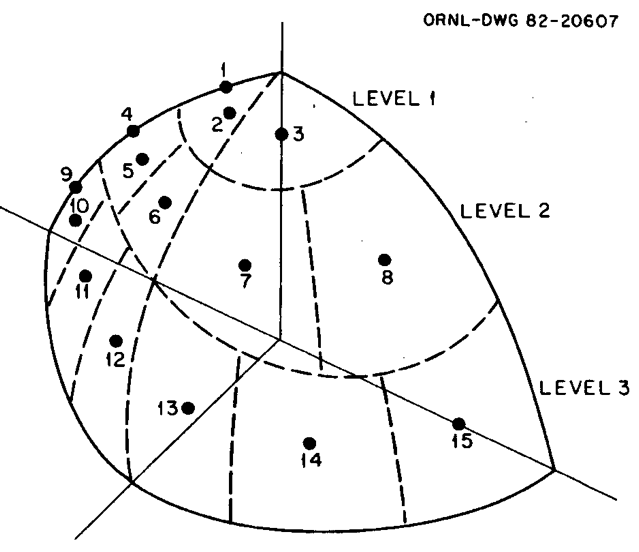
Fig. 9.1.7 Ordering of the directions for an S6 cylindrical set.
In general, an nth order quadrature will contain n(n + 4)/4 angles. The cosines, \(\mu\), and the weights are stored in two arrays internally in the code; and, since the weights for the 1st, 4th, and 9th angles are zero, the cosines for the corresponding levels are placed in these locations in the arrays.
The cylindrical sets are based on Gauss-Tschebyscheff schemes as recommended by [XSDEme75] with Gaussian quadratures in \(\beta\) and Tschebyscheff quadratures in \(\alpha\).
9.1.2.5. Weighted-difference formulation for discrete-ordinates equations
In order to solve the discrete-ordinates equations, an assumption is required concerning the relationship of the various flux terms: \(\psi_{i, m}, \psi_{i+1, m}, \psi_{i+1 / 2, m}, \psi_{i, m-1 / 2}, \psi_{i+1, m-1 / 2}\).
The solution of the equations involves three major loops: an outer loop over energy groups, a loop over angles, and a loop over the spatial mesh. The spatial loop is made either from the origin to the outside boundary or from the outside to the origin, depending on whether the angle is directed outward or inward, respectively.
Two models are widely used for expressing flux relationships: (1) the step model and (2) the diamond-difference linear model.
The “step model” is a histogram model whereby one sets the centered flux value to the appropriate boundary value, depending on which way the mesh sweep is going. If, for example, the sweep is to the right in space, then
or if to the left,
Likewise, in angle:
The step model involves a very crude approximation, but has the marked advantage of helping to ensure positivity of flux values as long as scattering sources are positive.
In the “diamond-difference” model, the centered fluxes are assumed linear with the edge values:
Unfortunately, though the linear model is clearly a better model than the step model, care must be taken by selecting a fine spatial mesh, or the linear extrapolation can lead to negative flux values. In some cases, the situation is so severe that it is impractical to take enough mesh points to eliminate the problems. Because of these difficulties XSDRNPM uses a different approach, as described below.
The weighted diamond difference model [XSDREJ77] was developed in an attempt to take advantage of the “correctness” of the linear model, while retaining the positive flux advantages of the step model.
A solution in some \(S_n\) codes is to use the linear model in all cases where positive fluxes are obtained and to revert to step model otherwise. Unfortunately, this method leads to artificial distortions in the fluxes.
Note that if one writes
that the same expression can be used to express linear or step model (e.g., \(a = b = \frac{1}{2}\) is equivalent to linear, while \(a = b = 1.0\) can be used for the step model).
In the weighted model, the intention is to use the linear model when fluxes are positive but to select values for a and b in the range
that ensure positivity, if the source is positive.
At this point, it is convenient to rewrite the discrete-ordinates expression in a simplified notation, without the obvious subscripts on energy group, angle, etc.
Combining Eqs. Eq. (9.1.43) and Eq. (9.1.40) or Eq. (9.1.41) yields the following expressions for \(\psi_{1+1}\) and \(\psi_{m+1 / 2}\):
where
In determining a and b, the “theta-weighted” model uses arbitrary multipliers \(\theta\)s on SV and \(\theta\)n on the \(C_2\) \(\psi_{m-\frac{1}{2}}\) or \(C_1\ \psi_i\) terms in Eqs. Eq. (9.1.44) and Eq. (9.1.45). (In [XSDTREJ80], a thorough discussion is given on the history of using different choices of \(\theta_s\) and \(\theta_n\) and the advantages and disadvantages of each method.) In XSDRNPM, a value of 0.9 is used for \(\theta_s\) and \(\theta_n\) following the practice in the DOT-IV code.7
For \(\psi_{i+1}\) in Eq. Eq. (9.1.44) to be positive, the numerator should be positive, thereby requiring
which in the \(\theta\)-weighted case becomes
A similar expression can be written for b using Eq. Eq. (9.1.45).
For reasons of accuracy, it is desirable to use \(a=b=\frac{1}{2}\). Therefore, when a or b is determined to be less than \(xfrac{1}{2}\) it is automatically set to \(xfrac{1}{2}\).
9.1.2.6. Boundary conditions
XSDRNPM allows a boundary condition to be specified for each of the two “outside” boundaries of its 1-D geometries. The options are the following:
1. Vacuum boundary – all angular fluxes that are directed inward at the boundary are set to zero (e.g., at the left-hand boundary of slab, \(\psi \left( \mu > 0 \right) = 0\), etc.).
2. Reflected boundary – the incoming angular flux at a boundary is set equal to the outgoing angular flux in the reflected direction (e.g., at the left-hand boundary of a slab),
3. Periodic boundary – the incoming angular flux at a boundary is set equal to the outgoing angular flux in the same angle at the opposite boundary.
4. White boundary – the angular fluxes of all incoming angles on a boundary are set equal to a constant value such that the net flow across the boundary is zero, that is,
This boundary condition is generally used as an outer-boundary condition for cell calculation of cylinders and spheres that occur in lattice geometries.
5. Albedo boundary – this option is for the white boundary condition except that a user-supplied group-dependent albedo multiplies the incoming angular fluxes. This option is rarely used, as it is difficult to relate to most practical situations.
9.1.2.7. Fixed sources
Two types of inhomogeneous or fixed sources can be specified in XSDRNPM.
In the first case, an isotropic group-dependent volumetric source can be specified for any or all spatial intervals in a system.
In the second case, an angle- and group-dependent boundary source can be specified for any or all boundaries between spatial intervals in a system, excepting the left-most boundary. In this case, one specifies not a source but a flux condition on the boundary. If one uses the “track length” definition for flux, it is easy to show that the flux condition is related to a source condition by
(This equation says that an isotropic source on a boundary would be input as a constant divided by the cosine of the direction.)
In conventional fixed-source calculations, the total fixed source in the system can be normalized to an input parameter, XNF. In the volumetric source case, the source values will be normalized such that
and in the boundary source case,
In the case where both volumetric and boundary sources are specified, the two sums are normalized to XNF.
The fixed source for a generalized adjoint calculation corresponds to a particular response ratio of interest. The generalized adjoint equation only has a solution for responses that are ratios of linear functionals of the flux, and in this case the source will contain both positive and negative components. These types of sources are described in more detail in ref:9-1-2-15-1 and in the SAMS chapter, in Generalized Perturbation Theory.
9.1.2.8. Dimension search calculations
XSDRNPM has three options for searching for dimensions such that the system will produce a specified effective multiplication factor, keff. The options are selected by a parameter IEVT in the 1$ array and are as follows:
zone width search (IEVT = 4),
outer radius search (IEVT = 5),
buckling search (IEVT = 6).
By default, the search is made to produce a keff value of unity. For keff’s other than unity, IPVT (3$ array) is set to unity and the desired keff is input as PV (5* array).
Other input parameters which apply specifically to all search calculations are in the 5* array and are EV, the starting eigenvalue guess, EVM, the eigenvalue modifier, EQL, the eigenvalue convergence, and XNPM, the new parameter modifier. These parameters are discussed in more detail below.
9.1.2.8.1. Zone-width search (IEVT = 4)
With this option, one can vary the width of any or all zones in a case. Note that it is also possible to change zone widths at different rates.
This option requires the inputting of a zone width modifier array (41*) which is used to specify the relative movements of the zones according to the following expression:
where \(\Delta Z_{j}^{i}, \Delta Z_{j}^{f}\) are the initial and final widths of zone j, respectively, ZMj is the zone width modifier for the zone (as input in the 41* array), and EV is the final “eigenvalue” for the problem. Note that a zero value for ZM will specify a fixed zone width. Negative values for ZM are allowed.
9.1.2.8.2. Outer radius search (IEVT = 5)
With this option, all zones are scaled uniformly in order to make the system attain the specified keff. The final zone widths are found by multiplying the initial values by the final “eigenvalue:”
9.1.2.8.3. Buckling search (IEVT = 6)
This option is used to search for “transverse” dimensions that will yield a specified keff for a system. This means that the search is for the height for a 1-D cylinder or the y- and/or z-dimensions in a 1-D slab.
For this option, the final dimensions are given by
DY = DY0 \(\times\) EV,
and
DZ = DZ0 \(\times\) EV,
where DY0 , DZ0 are the initial dimensions input in the 5* array.
9.1.2.8.4. Search calculation strategy
All the “dimension searches” use the same simple strategy. The calculations start by using the input eigenvalue (EV from the 5* array) to determine initial dimensions for the system. These dimensions allow the code to calculate a keff . The eigenvalue modifier (EVM in the 5* array) is then used to change the dimensions as follows:
IOPT = 4 (Zone width search)
IOPT = 5 (Outer radius search)
IOPT = 6 (Buckling search)
DY = DY0 (EV + EVM)
DZ = DZ0 (EV + EVM).
The new dimensions are then used in a new calculation which determines a second keff value.
XSDRNPM searches for a unity value of keff by default; however, when IPVT = 1 (3$ array), a nonunity value can be specified in PV (5* array) and the search will be made on this value.
Once the two keff’s are known, which are based on eigenvalues of EV and EV + EVM, respectively, a linear fit is used to project to the next value for EV. This yields an expression of the form
where k1 and k2 are the first and second value of keff , respectively. After this iteration, the procedure is to fit a quadratic to the three most recent keff values in order to obtain an estimate for the next EV.
The procedure continues until a relative convergence of EQL (5* array) or better is obtained on EV.
To prevent oscillations in the search, extrapolations are limited by XNPM, the new parameter modifier from the 5* array.
9.1.2.9. Alpa Search
It is possible to make some of the searches described in Sect. 9.1.2.8 in a more “direct” fashion than the strategy described in Sect. 9.1.2.8.4. XSDRNPM has two such options: (1) the alpha search and (2) a direct buckling search. These are described below.
9.1.2.9.1. Alpha search
The time-dependent form of the Boltzmann equation is identical with Eq. Eq. (9.1.1), except for the inclusion of a time-gradient term on the left-hand side:
All other flux terms in the expression also would include the time (t) argument.
In some analyses it is reasonable to assume that the time variation of the flux is exponential, that is,
When this variation is introduced into the expanded form of Eq. Eq. (9.1.1), the exponential terms all cancel leaving a leading term:
which is in the same form as the \(\Sigma_t \psi\) term.
If one considers integrating over energy, angle, and space, the following expression can be derived:
where
where
P \(\equiv\) production in the system,
A \(\equiv\) absorptions in the system,
L \(\equiv\) leakage from the system,
V \(\equiv\) \(\int_{0}^{\infty} d E \int_{0}^{4 \pi} d \overset{\rightharpoonup}{\Omega} \int_{s y s t e m} d \overset{\rightharpoonup}{r} \frac{\psi(\overset{\rightharpoonup}{r}, E, \overset{\rightharpoonup}{\Omega})}{\mathrm{v}}\)
Since all terms other than \(\alpha\) can be determined from a calculation, it is possible to determine \(\alpha\) directly, thereby avoiding a scheme like that used for dimension searches. In the balance expression, the fission component of the production term is adjusted for the case of a non-unity keff value (IPVT = 1 in the 3$ array).
An \(\alpha\)-search has several practical applications. If, for example, a subcritical assembly is pulsed by a source, the time-dependence of the flux is expected to die off exponentially. Another way to interpret the \(\alpha\)-search is as that amount of 1/v absorber which could be added or taken away from a system in order to achieve criticality. This number could be of interest when certain control materials are used, such as 10B5 , which is a “1/v” material.
9.1.2.9.2. Direct-buckling search
A “direct”-buckling search can be made using a procedure analogous to that described in Sect. 9.1.2.9.1. Recall that the buckling is introduced in order to represent a transverse leakage through the use of a DB2 \(\psi\) term. This suggests that the foregoing balance expression be written:
where
In this case, the diffusion coefficients, Dg, are determined from
where
and \(\Sigma\)1 is the within-group term from the P1 scattering matrixes:
The original B2 value is determined as specified in Sect. 9.1.2.12, and the \(\alpha\) is the square of the search parameter, that one multiplies by the original B2 value in order to determine the final buckling and, hence, the dimensions of the system.
9.1.2.10. Iteration and convergence tests
Two parameters are used to specify the required levels of convergence on an XSDRNPM calculation. These are EPS and PTC, both given in the 5* array. The flux calculations proceed through a series of iterations until either convergence is achieved or the specified iteration limit is exceeded.
The basic iteration strategy in XSDRNPM is now described. The discrete-ordinates difference equation is solved for the first angle and the first energy group. This sweep generally is made from the last interval boundary to the center of the system, and it uses the flux guess supplied as part of the input along with the boundary conditions. The second angle is then calculated, etc., until all angles in the quadrature are treated. At the end of this sweep, new scalar fluxes for the midpoints of all intervals have been determined. The angular sweep continues until either the point scalar fluxes are converged to within PTC or until the code makes IIM inner iterations. An exception to this “inner iteration” pattern occurs on the first outer (defined below) iteration whenever a fission density guess is used, instead of the flux guess. In this case, the program uses 1-D diffusion theory to determine a scalar flux value for all intervals and the angular sweeps are not made until the second outer iteration. After the first group is completed, the calculation goes to the second group and repeats the above procedure. This continues until all groups have been treated.
The pass through all groups, angles, and intervals is called an outer iteration. Most of the convergence checks on the outer iteration have to do with reaction rates involving all energy groups and are made against the EPS parameter mentioned above. For a coupled neutron-gamma problem, outer iterations are only performed for the neutron groups until convergence is achieved, then the final converged pass is made over all groups. In discussing these checks, it is convenient to define several terms:
Q \(\equiv\) total fixed source in the system
F \(\equiv\) total fission source in the system
D \(\equiv\) total outscatter rate in the system
D \(\equiv\) \(\sum_{i}^{intervals} \sum_{g}^{groups } \sum^{groups}_{\mathrm{g}^{\prime} \neq \mathrm{g}} \psi_{i, g} \sigma_{g \rightarrow g^{\prime}} \mathrm{V}_{\mathrm{i}}\)
\(\psi_{i, g}\) \(\equiv\) scalar flux in intervals i and group g
\(\sigma_{g \rightarrow g^{\prime}}\) \(\equiv\) macroscopic scattering cross section from group g to group
\(\mathrm{V}_{\mathrm{i}}\) \(\equiv\) volume of interval i
k \(\equiv\) outer iteration number
IGM \(\equiv\) total number of energy groups
\(\lambda_{k}\) \(\equiv\) \(\frac{Q+F_{k}}{Q+F_{k-1}}\)
\(G_{k}\) \(\equiv\) \(\frac{D_{k}}{Q+F_{k}}\)
\(\lambda_{k}^{\prime}\) \(\equiv\) \(\frac{G_{k-1}}{G_{k}}\)
\(U_{k}\) \(\equiv\) total upscatter rate = \(\sum_{i} \sum_{g} \sum_{g^{\prime}<g} \psi_{i, g} \sigma_{g \rightarrow g^{\prime}} \mathrm{V}_{i}\)
\(\lambda_{k}^{\prime \prime}\) \(\equiv\) \(U_{K} / U_{k-1}, U_{k-1} \neq 0_{j}=1, U_{k-1}=0\)
An inner iteration in XSDRNPM consists of sweeping one time through the entire spatial mesh for all the Sn angles for one energy group. When the fluxes for a particular group are being calculated, inner iterations (j) will continue until (a) the number of inner iterations for this outer iteration exceeds IIM (the inner iteration maximum) or (b) until
- (9.1.72)\[\max _{i}\left|\frac{\psi_{i, g}^{j}-\psi_{i, g}^{j-1}}{\psi_{i, g}^{j}}\right| \leq P T C\]
At the end of an outer iteration, the following checks are made:
- (9.1.73)\[\left|1.0-\lambda_{k}\right| \leq E P S\]
- (9.1.74)\[R\left|1.0-\lambda_{k}^{\prime}\right| \leq E P S\]
- (9.1.75)\[R\left|1.0-\lambda_{k}^{\prime \prime}\right| \leq E P S\]
R is a convergence relaxation factor and is set internally to 0.5 in XSDRNPM. If all convergence criteria are met, if ICM (the outer iteration maximum) is reached, or if ITMX (the maximum execution time) is exceeded, the problem will be terminated with full output; otherwise, another outer iteration will be started.
9.1.2.11. Group banding (scaling rebalance)
As described above, the normal mode of operation in XSDRNPM is to do inner iterations on a group until it converges, then go to the next group. For groups where there is no upscatter, the scattering source to a group depends only on higher energy groups for which the fluxes have already been calculated. A fixed source problem with no fission and no upscattering can, therefore, be converged in one outer iteration. Since fission sources and upscattering sources are calculated with fluxes from the previous outer iteration, multiple outer iterations must be done to converge problems involving these kinds of sources. For problems involving many fine thermal groups (groups with both upscatter and downscatter), a special convergence problem arises. Because the groups are fine, within-group scattering is small and the flux calculation is dominated by scattering sources from other groups. This situation leads to a very slow reduction in scattering source errors from one outer iteration to the next. XSDRNPM has a special “group banding” option for treating this problem. It involves collecting several groups together into a band and doing one inner for each group in the band while collecting particle balance information. This balance information is then used to solve for one set of flux rebalance factors to apply to each group in the band. Because the band is much wider than an individual group, the scattering that remains within the band is a much larger fraction of the total scattering source for the band. This condition leads to considerably faster convergence from one outer iteration to the next. The group banding option in XSDRNPM is triggered by the seventh entry in the 2$ array. The absolute value of this entry indicates the number of bands to be used. If the number is negative, these bands are only for the thermal groups. Normally there is no need to band together groups other than the thermal groups. An entry of -1 indicates that all the thermal groups will be treated as one band. This mode is one that is used successfully for many problems, but occasionally will cause a problem to not converge. For these problems using two or three bands for the thermal groups has been successful.
The code generates a default banding structure, but this structure can be overridden by inputting a 52$ array.
9.1.2.12. Buckling correction
XSDRNPM allows “buckling” corrections to be made for the transverse (non-calculated) dimensions in its 1-D slab and cylindrical geometries. Three input parameters-DY, DZ, and BF (5* array)-may be involved.
In the case of the 1-D slab, the height DY and the width DZ can be input. The buckling correction uses an expression based on asymptotic diffusion theory to account for leakage in the transverse direction and is treated analogous to an absorption cross section, that is,
Transverse Leakage \(=D B^{2} \psi\)
where B is the geometric buckling and is given by
and Y and Z are the height and width of the slab, respectively, and include extrapolation distances.
Recall that the “extrapolation distance” is defined as the linear extrapolation distance such that if one extrapolated to a zero flux value at this distance from the boundary, the interior flux shape in the body would be correctly represented. The distance can be shown to occur at 0.71\(\lambda_{t r}\), where \(\lambda_{t r}\) is the transport mean free path given by \(1 / \Sigma_{t r}\). Note that for a slab, there are two extrapolation distances to include (one on either side) for the height and width, such that
and
The 1.42 factor (= 2 X 0.71) is input in the BF parameter of the 5* array.
In calculating \(\lambda_{tr}\), a transport cross section, \(\Sigma_{tr}\), is determined from
which varies as a function of energy group and zone. The \(\Sigma_{s 1}\) term is the within-group term from the P1 scattering matrix.
In the case of the 1-D cylinder, the procedure is the same as for the slab except that the buckling is determined from
since only one transverse dimension is needed.
The diffusion coefficient in the leakage term is determined from
Note that when comparing with codes or treatments using a fixed value of buckling for every group, a user can force this situation in XSDRNPM by inputting a zero value for BF and DZ and setting DY to determine the required buckling value.
9.1.2.13. Void streaming correction
In real slab and cylindrical geometries, void regions offer streaming paths that are nonexistent in the 1-D cases with quadratures that do not include a vertical angle. A correction for this effect has been suggested by Olsen [XSDOls65], who uses an adjustment to the absorption cross section to account for the transverse leakage.
If one considers a slab of height H, the void streaming correction is introduced through an adjustment to the total cross section and is given by
where \(\mu_m\) is the cosine of the direction.
In the case of a cylinder of height H, the adjustment is
These streaming corrections are very approximate and do not properly account for the fact that the streaming is enhanced near the ends of a void channel; however, they are probably better than the alternative, which is to make no correction at all.
9.1.2.14. Cross-section weighting
XSDRNPM weights cross sections according to the following four options:
“Cell” weighting,
“Zone” weighting,
“Region” or “vein” weighting, and
“Inner cell” weighting.
In all cases the “averaged” cross sections are defined in a manner that conserves reaction rates, that is,
where
\(\bar{\sigma}_{G}\) \(\equiv\) average cross section in group G,
\(N_{D}(r)\) \(\equiv\) number density used in the definition for the weighting option selected,
\(\psi(E, r)\) \(\equiv\) weighting spectrum,
\(N(r)\) \(\equiv\) real number density as a function of spatial position,
\(\sigma(E, r)\) \(\equiv\) cross section in unreduced form.
If we convert to multigroup notation and use W for the weighting spectrum (instead of \(\psi\)), Eq. Eq. (9.1.84) becomes
9.1.2.14.1. “Cell Weighting”
Cell weighting is consistent with homogenizing the cross sections in a heterogeneous cell. This is the recommended option to prepare cross sections for a real reactor calculation that will be made with a 2- or 3-D model of the reactor. Most of these codes have no provisions for explicitly representing individual fuel pins which are interspersed in a moderator region.
Cell-weighted cross sections are defined in a manner that attempts to preserve the reaction rates which occur in a representative cell from the reactor. In Eq. Eq. (9.1.85) the weighting involves the following substitution:
where
V j \(\equiv\) volume of zone j.
9.1.2.14.2. “Zone” weighting
Zone weighting is the simplest of the three XSDRNPM weighting options. Each zone produces a unique set of cross sections which preserves reaction rates for the zone. In Eq. Eq. (9.1.85), the spatial sum is over the zone considered, and N j \(N_{D}^{j}\) and are unity.
Zone weighting is used very frequently, especially for problems whose collapsed cross sections are to be used in a problem whose geometrical and material layout is similar to that in the weighting problem.
9.1.2.14.3. “Region” weighting
“Region-” or “vein-” weighted cross sections are weighted “where-the-nuclide-is.” In most problems, there are nuclides of secondary importance which do not need a separate “zone-weighted” set for every region in which the nuclide occurs. Examples are the components of stainless steel. Stainless steel is encountered in a variety of locations and flux environments, but generally one set of cross sections for iron, chromium, manganese, nickel, etc., will suffice for most reactor calculations.
In Eq. Eq. (9.1.85), the spatial sum is over all zones which contain the nuclide of interest with
9.1.2.14.4. “Inner-cell” weighting
For inner-cell weighting, cell weighting is performed over specified innermost regions in the problem. Nuclides outside these regions are not weighted.
This option is generally employed as follows: A “cell” is described in exactly the same manner as for cell weighting (Sect. 9.1.2.14.1) except that in this case it is surrounded by a homogeneous representation for the remainder of the core and by blankets, reflectors, etc. The flux calculation is made over this complete system, which should have a more realistic treatment of the leakage across the outer boundary of the interior cell. The cell weighting is subsequently made only over the interior cell.
9.1.2.14.5. Multigroup weighting equations
Cell weighting
where
Zone weighting
Region weighting
9.1.2.14.6. Transfer matrices
Collapsing transfer matrices is not quite so simple as collapsing cross sections with a single value per group. A group-to-group term in the broad group sense conserves the scattering rate from one group to the other, that is,
where the asterisk (*) denotes that the number density on the left side of the equation is consistent with the weighting desired. Therefore, the multigroup forms of the weighting equations for components of the transfer matrices are as follows:
Cell weighting
Zone weighting
Region weighting
Theoretically, the higher-than-zero order \(\sigma_{l}\left(g \rightarrow g^{\prime}\right)\) should be weighted over \(\psi_l\). Since these functions are generally positive-negative, \(\psi_l\) weighting does not always work in practice, and XSDRNPM weights the \(\sigma_{l}\left(g \rightarrow g^{\prime}\right), \quad>0\), by the scalar flux, which is positive. This procedure gives usable values for most cases.
9.1.2.14.7. Weighting of \(\bar{v}\)
In weighting parameters such as \(\bar{v}\), the average number of neutrons produced per fission, one is interested in preserving the fission source; therefore, the weighting is over \(\sigma_f \psi\) instead of just \(\psi\). The weighting procedure in XSDRNPM is to calculate \(\left(\overline{v \sigma_{f}}\right)_{G}\) and (\(\sigma_f\))G using the appropriate choice from Eqs. Eq. (9.1.95), Eq. (9.1.96), or Eq. (9.1.97). Then
9.1.2.14.8. Transport cross sections
Transport cross sections are not as directly related to the physical properties of a material as much as other group-averaged values. Instead of a reaction rate, these numbers must attempt to preserve a “flux gradient,” which not only depends on the cross sections of the material, but is also very strongly influenced by the geometry and the other nuclides in the vicinity of a material.
Two options are provided in XSDRNPM to generate transport cross sections-options based on the “consistent” and “inconsistent” methods for solving the Pl transport equations. These approximations are referred to as the “outscatter” and “inscatter” approximations because of the nature of the equations used.
9.1.2.14.8.1. Outscatter approximation (inconsistent method)
In the outscatter approximation, the assumption is made that
When one notes that
and that
where the \(\sigma_{l}\left(g \rightarrow g^{\prime}\right)\) terms are the P1 coefficients of the scattering matrix, the origin of the term “outscatter” to designate the approximation is evident.
9.1.2.14.8.2. Inscatter approximation (consistent method)
In the “consistent” solution of the P1 point transport equations, it can be shown that
where \(J\left(E^{\prime}\right)\) is the current.
If one multiplies the equation by J(E), integrates over group g, and converts to group-averaged form by dividing by \(\int_{g} J(E) d E\) the following expression is derived:
This is the “inscatter” approximation. It is consistent because the transport values are explicitly derived from the P0 and P1 equations. As a general rule, the transport values from this treatment are “better” than those from the “inconsistent” treatment. However, in some cases (notably hydrogen at lower energies), negative numbers may be calculated which are unusable and the more approximate approach must be used.
9.1.2.14.8.3. Weighting function for transport cross section
Unfortunately, the matter of choosing a current to use in the “transport” weighting is not simple. In real problems, currents are positive-negative as a function of energy and space. When cross sections are averaged over positive-negative functions, the “law-of-the-mean” no longer holds and the average value can be anything. This unbounded nature leads to real problems in diffusion calculations.
Approximations that inherently guarantee positive currents are generally used in other codes that circumvent the positive-negative problem. For example, in Bn theory the current is given by
where B and \(\psi\) are both positive.
In XSDRNPM, more direct routes that ensure positivity are taken (e.g., one might set \(\mathrm{W}_{\mathrm{g}} \equiv\left|\mathrm{W}_{\mathrm{g}}\right|\)). This is crudely supported by the following argument:
Consider a 1-D cylindrical calculation. In two dimensions, the current is a vector combination, that is,
In XSDRNPM, the z direction is treated by using a buckling approximation, that is,
In the weighting calculation, we want to weight over the magnitude of the current. In XSDRNPM, the z current is imaginary, since we are not calculating a z-direction:
The magnitude of a complex quantity is
which is always positive.
In a discrete-ordinates calculation, the current is easily obtained since it is the first flux moment.
XSDRNPM has the following options for calculating the current:
The first option is the recommended option; option 2 treats only the current in the primary direction; option 3 will always be positive and is a weighting over the total leakage from the system. Option 4 is sometimes referred to as a “bootstrap” approximation; option 5 is equivalent to that used in codes that employ \(B_n\) theory.
Once the currents are determined, the transport values are determined as set forth in the equations discussed above. For example, consider cell weighting and the “inscatter” approximation,
For cell weighting and the “outscatter” approximation,
9.1.2.15. Adjoint calculations
XSDRNPM will, upon option, solve the adjoint forms of the 1-D transport equation.
Several special procedures apply for the adjoint calculation:
The iteration pattern discussed in Sect. 9.1.2.10 is reversed in energy. The scheme starts with the last (lowest energy) group and proceeds to the first group.
The angular quadrature is treated as if it has the reverse directions associated with the angle (e.g., many quadratures start with \(\mu_1=-1.0\)). In the adjoint case, this direction is for \(\mu_1 = +1.0\).
All edits of input fluxes and collapsed cross sections are given in their normal ordering, as opposed to many codes which require their reversal.
Adjoint calculations have many uses and advantages. As opposed to the forward calculation which yields particle density values, the adjoint fluxes are more abstract and can be thought of as particle importance.
Consider, for example, the problem of determining the response of a detector to particles as a function of their energy and direction. Assume the detector is a cylindrical fission chamber that utilizes a foil of 235U. The most obvious way to attack this problem is to mock up the detector and make a series of runs that contain sources of identical strength in different angles and energy groups. If an S8 (24 angles) quadrature were used with 50 energy groups, the 12 \(\times\) 50 or 600 independent calculations could be used to completely determine the responses. (Here we have taken note that half of the angles will point away from a detector and, hence, produce no response.) The adjoint calculation produces all 600 responses in one run that is no more difficult and time consuming than the typical forward case. In the adjoint case, the detector response (i.e., the fission cross section of 235U would be specified as a source in the foil region and the adjoint fluxes given as a function of energy and angle would be interpreted as the source of neutrons necessary to produce a response of the magnitude to which one required the response to be normalized.
A second important use of adjoint calculations is to establish good biasing factors for Monte Carlo codes. Two recent reports [XSDHof82, XSDHT82] discuss the time and accuracy advantages of this approach for shielding and criticality applications and give some real examples as to how to make the calculations.
Perturbation theory uses adjoint and forward fluxes in combination in a manner that determines changes in responses that would arise from changing parameters used in a calculation. One [XSDWRHB79] interesting application is to determine the sensitivity of a calculation to changes in one or more cross-section value changes.
9.1.2.15.1. Generalized adjoint calculations
Generalized adjoint solutions are needed for generalized perturbation theory (GPT) applications such as sensitivity and uncertainty analysis. The generalized adjoint solution differs from both a conventional external source case and a fundamental mode eigenvalue calculation: It has the transport operator for an adjoint eigenvalue equation, but contains a fixed source term as well. The eigenvalue transport operator is singular, which forces certain restrictions on the allowable sources. The generalized adjoint source term is associated with a particular response ratio of interest in a critical system, such as
where HN and HD are response functions defining the response of interest and \(\psi_{i, g}\) is the scalar flux from a prior forward eigenvalue solution of the same problem. The generalized adjoint source for this response is defined as
The above source expression is computed automatically whenever XSDRN is executed in the TSUNAMI-1D sequence, but must it be computed and input by the user if XSDRN is run standalone for a generalized adjoint case.
In order to obtain a unique solution and avoid numerical problems, the generalized adjoint solution is “normalized” to contain no fundamental harmonic of the adjoint eigenvalue calculation. This is done by sweeping out the adjoint fundamental mode “contamination” from the fission source after each outer iteration, as described in the SAMS chapter, in Generalized Perturbation Theory. This operation requires both forward and adjoint eigenvalue solutions from prior XSDRN calculations. External files containing the fundamental mode forward and adjoint fluxes are input to the generalized adjoint calculation.
Unlike conventional fixed source and eigenvalue calculations, the generalized adjoint flux has both negative and positive components. This causes some XSDRN acceleration features such as space-dependent rebalance and group-banding to not function properly; and thus these are turned off internally. Typically the outer iterations for generalized adjoint solution converge much slower than an eigenvalue calculation. More background on GPT and generalized adjoint properties can be found in [XSDWil86].
9.1.2.16. Coupled neutron-photon calculations
In XSDRNPM, it is possible to do a neutron or a photon calculation, depending only on whether the input libraries are for neutrons or gamma rays. It is also possible to do a “coupled neutron-photon” calculation which automatically determines the gamma-ray sources arising from neutron induced interactions in its photon calculation. This calculation, of course, requires an input cross-section library containing three classes of data:
neutron cross sections, including neutron-to-neutron transfer matrices,
photon production cross sections (i.e., neutron-to-gamma transfer matrices), and
gamma-ray cross sections, including gamma-ray-to-gamma-ray transfer matrices.
At present there are no provisions for treating neutrons produced from gamma interactions other than having the user introduce these sources by hand in a sort of iterative procedure, though this reaction is certainly not unknown (cf., deuterium, beryllium-9, and carbon-13). There are several cases where the (\(\gamma,n\)) interaction can be important. If, for example, one looks at neutrons in a water-moderated pool reactor or in a water spent fuel storage tank at large distances from the fuel, the dominant source is from the neutrons produced by the deuterium in the water.
Normally the neutron-photon calculation requires no more input than a single particle run, except in the case where extraneous neutron and/or gamma-ray sources need to be specified. Most output edits will be split into a neutron and a gamma-ray part and will be labeled as such
9.1.2.17. Diffusion theory option
XSDRNPM can make a 1-D diffusion theory calculation in user-specified energy groups (enter 1’s for the appropriate groups of the 46$ array). In this case, the P1 diffusion equations [XSDAld63] are solved:
where
Solving Eq. Eq. (9.1.118) for \(\psi_{0, I+1}\) and substituting into Eq. Eq. (9.1.119), one can write
Solving Eq. Eq. (9.1.119) for \(\psi_{1, I}\) and substituting into Eq. Eq. (9.1.118) , one can write
If one assumes
and plugs Eqs. Eq. (9.1.127) and Eq. (9.1.128) into , solving for \(\psi_{1, I}\) yields:
which by inspection and comparison with Eq. Eq. (9.1.130) gives expressions for PI and qI.
Equations Eq. (9.1.129) and Eq. (9.1.130) can be substituted into Eq. Eq. (9.1.118) and solved for \(\psi_{0, I+1}\):
which is the expression used in XSDRNPM. The procedure solves for arrays of PI and qI which are plugged back into the above expression to yield the fluxes.
9.1.2.18. Infinite-medium theory option
It is possible to force the flux calculation in XSDRNPM to use an infinite medium option for any or all energy groups by entering 2’s in the appropriate positions in the 46$ array. When a multiregion calculation is requested, the program will first determine spatially averaged cross sections to use in the infinite-medium expression and then place the infinite-medium flux in all spatial regions for use in any subsequent calculations, such as cross-section weighting. All higher flux moments are set to zero.
The balance expression is
where Fg is the fission source in group g, Sg is the sum of any fixed source and inscattering source, and \(\sum_{t}^{g}\) and \(\Sigma(\mathrm{g} \rightarrow \mathrm{g})\) are homogenized total and group-to-group scattering cross sections.
9.1.2.19. BN theory option
XSDRNPM can make a \(B_n\) calculation in user-specified energy groups (enter 3’s for the appropriate groups of the 46$ array). As in the infinite-medium option discussed in Sect. 9.1.2.18, cross sections in a multiregion system are not homogenized.
The \(B_n\) equations [XSDHTS76] can be written
where \(\delta_{l}^{0}\) is the Kronecker delta function and QN is a Legendre polynomial of the second kind. In mutigroup form, the above expressions become:
In Eqs. Eq. (9.1.134) and Eq. (9.1.138), the S term includes fission, fixed, and scattering source components.
9.1.3. XSDRNPM Input Data
The input data to XSDRNPM consist of a title card and up to five data blocks, depending on the particular problem. All data in these blocks are entered using the FIDO formats discussed in the chapter on FIDO.
In the description that follows, the quantity in square brackets is the number of items in an array. The quantity in braces is the condition which requires the array to be input. If no condition is specified, an array must be input. Default parameters that are used if an array is not input are shown in parentheses if nonzero.
*******************************************************************
Title Card - Format (20A4)
This is the title card for the problem. It will be used to label the problem output.
Data Block 1
This block contains information to set up various array dimensions and most calculational and editing options. Various convergence criteria and special constants can be input.
0$$ Logical Assignments [17]
LPUN – Logical number for punched card output (7).
LRSF – Random-access scratch for fluxes (10).
LAWL – Input AMPX working library (4).
LANC – ANISN binary or CCCC ISOTXS library (20).
LOWL – Output weighted library (3).
LANG – Angular flux scratch file (16).
LSFF – Scalar flux output file (17).
LSF2 – Sequential scratch space (18).
LSF3 – Sequential scratch space (19).
LRSM – Random-access scratch for macroscopic cross sections (8).
LRSX – Random-access scratch for macroscopic cross sections (9).
LACF – Activities output file (75).
LBTF – Balance table output file (76).
LIDF – Input dump file (73).
LSEN – Sensitivity output file (6).
LEXT – Not used (0).
LISF – Scalar flux input guess file (0).
1$ General Problem Description [15]
IGE - problem geometry (1)
0 - homogeneous (This causes a BN calculation to be made for all zones – Sect. 9.1.2.19)
1 - slab
2 - cylinder
3 - sphere
IZM – number of separate material regions or zones. (1)
IM – number of spatial intervals in the problem. (1)
IBL – the boundary condition at the left-hand boundary of the system. (1)
0 - vacuum boundary
1 - reflected boundary
2 - periodic boundary
3 - white/albedo boundary
Boundary conditions are discussed in Sect. 9.1.2.6.
IBR - the boundary condition at the right-hand boundary of the system. (1)
0 - vacuum boundary
1 - reflected boundary
2 - periodic boundary
3 - white/albedo boundary
MXX – the number of compositions used in the problem mock-up.
MS – the number of entries in the mixing table which specifies the makeup of the MXX compositions.
ISN – the order of angular quadrature to be used. If ISN > 0, XSDRNPM will calculate an angular quadrature for the appropriate geometry. If ISN < 0, the calculation is bypassed, and the user must supply a set in the 42# and 43# arrays.
ISCT – the order of scattering. Flux moments will be calculated through this order.
IEVT – the type of calculation. (1)
0 - fixed source
1 - k calculation
2 - \(\alpha\) calculation (flux is assumed to have an \(e^{-\alpha t}\) time variation)
3 - inoperable in present version
4 - zone width search
5 - outer radius search
6 - buckling search
7 - direct buckling search
IIM – the inner iteration maximum used in an Sn calculation. (10)
ICM – the outer iteration maximum. (10)
After ICM outer iterations, the problem will be forced into the termination phase and the program will continue as if full convergence was attained. A message to this effect is printed.
ICLC – theory option. (0)
0 - use \(S_n\) theory always
N - use alternative theory (diffusion, infinite medium, or Bn) for N outer iterations, after which revert back to Sn theory.
-N - always use alternative theory
ITH – forward/adjoint selector. (0)
0 - solve the forward Boltzmann equation.
1 - solve the adjoint Boltzmann equation.
IFLU – Generalized adjoint calculation flag. (0)
0 - standard calculation
1 - Generalized adjoint calculation. Requires input forward and adjoint fundamental mode fluxes on units 31 and 32, respectively
2$ Editing and Special Options [10]
IPRT – fine-group mixture cross-section edits. (-1)
-2 - no edits
-1 - edit 1-D cross sections
0-N - edit through PN cross sections. 1-D edits are made, also.
ID1 – flux editing options. (0)
ID1
Angular fluxes
Scalar fluxes
Puncha
Scalar fluxes
-1
No
No
No
0
No
Yes
No
1
Yes
Yes
No
2
No
Yes
Yes
3
Yes
Yes
Yes
a The fluxes will be punched in a format suitable for restarting an XSDRNPM calculation.
IPBT – balance table edits. (0)
-1 - none
0 - make fine-group balance tables
1 - make fine- and broad-group balance tables
ISX – broad-group flux edit as a function of interval. (0) (0/1 = no/yes)
ISEN – outer iteration acceleration. Input a zero. (0)
IBLN – control number of outer iteration groups. (0)
NBANDS – number of flux rebalance bands. (0) < 0, then this is the number of bands in the thermal range.
IFSN – If > 0 means no fission source if IEVT=0. (0)
ISQ3 – sequence number of file opened on unit LOWL. (1)
IDM4 – not used. (0)
The structure of the “activity” and the “balance table” files are described in Appendix A.
3$ Various Options [12]
IFG – cross-section weighting. (0)
0 - none required
1 - collapse cross sections
IQM – volumetric sources. (0)
0 - none
N - N volumetric source spectra will be input in the 31* array
IPM – boundary sources. (0)
0 - none
N - N boundary source spectra will be input in the 32* array
IFN – starting guess. (0)
0 - flux guess (33# array)
1 - fission density guess (34# array)
ITMX – maximum time allowed for the flux calculation in minutes. A value of zero specifies that the calculation should not be terminated because of time; otherwise the problem will be forced into the termination phase when ITMX is exceeded. (0) Bear in mind that this is an internal timing check and has no connection with operator or system terminations due to excessive times.
IDAT1 – external data storage. (0)
0 - keep all arrays in core if possible
1 - store mixture cross sections externally on a direct access device
2 - store cross sections and fixed sources externally on direct access devices
IPN – diffusion coefficient option for transverse leakage corrections. (3)
0 - determine a transport cross section for each zone using P0 and P1 cross sections and, hence, a diffusion coefficient from 1/3 \(\Sigma\)tr.
1 - spatially average the diffusion coefficients determined as for the above option and use it for all zones.
2 - spatially average the transport cross sections for all zones and determine a diffusion coefficient to be used in all zones by taking one over three times this value.
3 - flux weight the transport cross sections for all zones and determine a diffusion coefficient to be used in all zones by taking one over three times this value.
Normally, the first option (IPN = 0) is adequate; however, in cases involving regions of low concentration (near void) and, hence, very low transport cross sections, the very large diffusion coefficients lead to nonphysical behavior. In this case, the IPN = 3 option has been demonstrated to operate the best.
IDFM – density factors. (0)
0 - none
1 - read in density factors in the 38* array
IAZ – activity calculation trigger. (0)
0 - none
N - calculate the reaction rates by material zone for N different processes specified in the 49$ and 50$ arrays
IAI – spatially dependent activity rates. (0)
0 - none
1 - calculate reaction rates in each interval for IAZ processes
IFCT – thermal upscatter scaling. (0)
0 - none
1 - use upscatter scaling for accelerated problem convergence
IPVT – parametric eigenvalue search. (0)
0 - none
1 - a search calculation will be made for an eigenvalue equal to PV
2 - an \(\alpha\) loss term with \(\alpha\) = PV will be added to the transport equation.
The term \(\alpha\) will depend on the IEVT option selected
4$ Cross-Section Weighting Options [XSDEme75] {IFG = 1}
Note
Currently XSDRNPM does not support outputting weighted cross section libraries in a format other than AMPX. The following items are still allowed to be entered into XSDRNPM input files for legacy inputs, but anything not relating to AMPX library format will have no effect.
ICON – type of weighting. (See Sect. 9.1.2.14)
- -N - inner cell (with N zones in the cell). Cell weighting is performed
over the N innermost regions in the problem. Nuclides outside these regions are not weighted.
-1 - cell
0 - zone
1 - region or vein
ITP – collapsed output format desired.
0-19 – cross sections are written only in the AMPX weighted library formats on logical 3. A weighted library is always written when IFG= 1. 20-29 – (deprecated feature). 30-39 – (deprecated feature). 40-49 – (deprecated feature).
The various values of ITP (modulo 10) are used to select the different transport cross-section weighting options mentioned earlier. The options are:
ITP = 0 => \(\sqrt{\left(\psi_{1}^{g}+\left(D G \psi_{g}\right)\right)^{2}}\)
ITP = 1 => absolute value of current
ITP = 2 => \(\mathrm{DB}^{2} \psi_{\mathrm{g}}+\) outside leakage
ITP = 3 => \(\psi / \sum_{\mathrm{t}}^{\mathrm{g}}\)
ITP = 4 => \(\mathrm{DB} \psi_{\mathrm{g}}\)
ITP = other values are reserved for future development and should not be used.
IPP – weighted cross-section edit option -1.
-2 – none
-1 – edit 1-D data
0-N – edit through PN cross-section arrays. 1-D edits are given.
IHTF – (deprecated feature)
NDSF – (deprecated feature)
NUSF – (deprecated feature)
IAP – (deprecated feature)
(deprecated feature)
5* Convergence Criteria and Assorted Constants [12]
EPS – overall problem convergence. (10:sup:-4)
PTC – scalar flux convergence. (10:sup:-5)
XNF – normalization factor. (1.0)
When IEVT = 0, the fixed sources are normalized to XNF.
For IEVT > 0, the fission source is normalized to XNF.
When XNF = 0.0, no normalization is made.
XNF should only be specified as 0 for a fixed source problem (IEVT = 0).
EV – starting eigenvalue guess for search calculations.
EVM – eigenvalue modifier used in a search calculation. The following is a tabulation of recommended values for EV and EVM.
IEVT
Calculation type
EV
EVM
0
Fixed source
0
0
1
k-calculation
0
0
2
Direct \(\alpha\)-search
0
0
3
–
–
–
4
Zone width search
0
-0.1
5
Outer radius search
Starting outer radius
-0.1*EV
6
Buckling search
1.0
-0.1
7
Direct buckling search
0.0
0.0
6. BF – buckling factor (1.420892). This parameter is two times the multiplier on the “extrapolation” distance used to determine where a linearly extrapolated line from the asymptotic flux shape would go to zero (e.g., for slabs, the extrapolation distance is \(0.71 \lambda_{t r}\) and, hence, BF 1.42).
7. DY – first transverse dimension in centimeters used in a buckling correction to calculate leakage normal to the principal calculation direction (i.e., the height of a slab or a cylinder).
8. DZ – second transverse dimension in centimeters used for a buckling correction (i.e., the width of a slab).
9. VSC – void streaming correction. This is the height of a void streaming path in a cylinder or slab in centimeters. See Sect. 9.1.2.13.
10. PV – parametric eigenvalue or value for \(\alpha\) used when IPVT > 0. When IPVT = 1 and IEVT > 1, this is the value of k-effective on which the search calculation is to be made (0.0)
EQL – eigenvalue convergence for a search. (10-3)
XNPM – new parameter modifier used in search calculations. (0.75)
T Terminate data block.
Data Block 2
This block contains information on the composition of the materials used in the calculation. Also included is an array to select special cross sections for ANISN and an array to identify cross sections written on the CCCC ISOTXS library.
Note
Currently XSDRNPM does not support outputting weighted cross section libraries in any format other than AMPX. XSDRNPM will still read the deprecated arrays, but they will have no effect.
10$ (deprecated array)
12$ (deprecated array)
11$ Composition Numbers in Mixing Table [MS]
If the input multigroup library was previously self-shielded by running the XSProc module, the composition numbers are the mix numbers given in the READ COMP block of XSProc. If the input library has not been previously self-shielded, enter all zeros.
Note
this is a new array added in SCALE 6.2 which MUST be present when using a microscopic library produced by the XSProc module. It may be omitted if using a macroscopic library from XSProc
13$ Local Mixture Numbers in Mixing Table [MS]
The values range from 1 to MXX, and are used only in XSDRN for referencing mixtures in the mixing table.
14$ Isotope Identifiers in Mixing Table [MS]
A set of data with this identification must be on unit LAWL, the XSDRNPM working library, though the code will not make checks to ensure this is the case.
15* Isotope Concentrations in Mixing Table [MS]
16$ (deprecated array)
18U (deprecated array)
T Terminate Data Block
Data Block 3 {IEVT = 0}
This block is used to specify fixed sources. ..
30$ Source Spectrum Number by Interval [IM]
31* Volumetric Source Spectra [IQM*IGM]
32* Surface Source Spectra [IPM*IGM*MM]
Each of the IQM or IPM spectra is specified in the 31* or 32* array and are stacked one after the other in that array. If both volumetric and surface sources are used in the same problem, the surface source number is multiplied by (IQM + 1) when entered in the 30$ array.
A volumetric spectrum will consist of IGM (number of energy groups) entries which are the relative integrated values of the source in each group.
A surface source is always assumed to be on the right-hand side of a spatial interval. It is input as was the volumetric source, except that each group contains entries for the MM angles in the \(S_n\) quadrature chosen for the problem. Note that a surface source is an integrated value and is actually a flux condition in the Sn|equations.
In the 30$ array, a zero entry specifies that no source is in an interval.
Data Block 4
This data block contains starting guesses for fluxes and fission densities. If fluxes are read from an external device (LISF>0), this data block is omitted. Both arrays in this block are double-precision arrays, which will require the use of the “#” array designator; otherwise the number of entries read into the arrays will be incorrect or may contain nonsensical values for the starting guess.
33# Flux Guess [IM*IGM] {IFN=0}
A guess for the scalar flux is specified in the order: ((FLUX(I,J),I=1,IM),J=1,IGM), where IM is the number of spatial intervals and IGM is the total number of energy groups. For fixed-source problems, without better information, use zeroes. For eigenvalue problems, a nonzero flux guess must be used. The fluxes punched by using the ID1 parameter in the 2$ array can be used here in restart calculations.
34# Fission Density Guess [IM] {IFN=1}
This is a guess at the number of fission neutrons produced in an interval. When IFN = 1, XSDRNPM uses diffusion theory for the first outer iteration, after which it reverts to the normal mode.
T Terminate this data block.
Data Block 5
This block contains the remaining data needed for an XSDRNPM calculation.
35* Interval Boundaries [IM+1] (cm)
This array describes the spatial quadrature into which the problem model is divided. The boundaries are nonnegative for curvilinear geometries and in increasing order. Usually they will start with a zero value, though this is not necessary. The origin for slab geometry may be negative.
36$ Zone Number for Each Spatial Interval [IM]
Spatial zones should be contiguous.
38* Density Factors by Interval [IM] {IDFM>0} (1.0)
These factors are used to effect a density variation in a mixture as a function of spatial interval. Zero for a density factor affords a convenient way for modeling a void region.
39$ Mixture Numbers by Zone [IZM]
The mixture that is in a zone is specified here.
40$ Order of Scattering by Zone [IZM] (ISCT)
This is the order, l, of the *Sn Pl *calculation which is desired in a zone. This number should be no larger than ISCT.
41* Radius Modifiers by Zone [IZM] {IEVT=4}
These parameters specify the relative movement of the width of a zone in a zone width search. A zero indicates that a zone’s width is fixed. (See Sect. 9.1.2.8)
42# Weights of the Angles in the Discrete-Ordinates Quadrature MM = ISN + 1 for slabs and spheres, ISN*(ISN + 4)/4 for a cylinder.
Input this set if you wish to override those provided by XSDRNPM. See Sect. 9.1.2.4.3, Sect. 9.1.2.4.4, or Sect. 9.1.2.4.5.
43# Cosines of the Angles in the Discrete-Ordinates Quadrature [MM]
Input this set if you wish to override those provided by XSDRNPM. See Sect. 9.1.2.4.3, Sect. 9.1.2.4.4, or Sect. 9.1.2.4.5.
46$ Calculational Option by Group [IGM] {ICLC>0}
0 - perform discrete-ordinates calculation for this group.
1 - perform a diffusion calculation for this group for ICLC outer iterations; use discrete-ordinates theory after this.
2 - perform a homogeneous calculation for this group for ICLC outer iterations; then revert back to discrete-ordinates theory.
3 - perform a homogeneous calculation using Bn theory for this group.
47* Right-Boundary Albedos by Group [IGM] {IBR=3} (1.0)
A right-boundary albedo is specified for each fine group. The return current is distributed isotropically in angle.
48* Left-Boundary Albedos by Group [IGM] {IBL=3} (1.0)
As for the 47* array but for the left boundary. Note that if IBR or IBL is 3 and the corresponding 47* or 48* array is omitted, XSDRNPM fills the array with 1.0’s effecting a boundary with zero net current and with isotropic neutron return.
49$ Material Number for Activities [IAZ] {IAZ>0}
50$ Process Number for Activities [IAZ] {IAZ>0}
The 49$ and 50$ arrays provide a means of obtaining the activity (reaction rate) for any process for which cross sections are available in the XSDRNPM calculation. A representative activity table entry is shown below:
ACTIVITY TABLE ENTRY
49$
50$
M
N
This entry specifies that the activity N for material M be calculated for all parts of the system which contain that material.
If N is < 0, a density of 1.0 is used to calculate activities instead of densities in the mixing table. Allowable process identifiers are given in Appendix M4.B.
If M is < 0, the activities by interval will be multiplied by a 1-D area as follows:
1.0 for a slab (IGE=1)
2 \(\times\) r for a cylinder (IGE=2)
4 \(\times\) r2 for a sphere (IGE=3)
51$ Broad-Group Numbers [IGM] {IFG>0}
This array contains the broad-group numbers into which the fine groups are collapsed in a flux-weighting calculation. For example, if the first five fine groups are to be collapsed to the first broad group, the first five entries in the 51$ array are 1, etc. A zero value can be used to ignore (or truncate) a group.
52$ Lower Band Group Numbers [NBANDS]
Group numbers giving the last group in a flux rebalance band. Overrides the default set supplied by XSDRNPM.
9.1.3.1. Abbreviated XSDRNPM input description
Title Card - (18A4) |
|
DATA BLOCK 1 |
|
-1$ - Storage Assignment 1. Maximum Length of Storage Array 0$- Logical Assignments [17] 1. Punched Cards (7) 2. Direct Access - Fluxes (10) 3. Working Library (4) 4. ANISN or ISOTXS (20) 5. Weighted Library (3) 6. Angular Fluxes (16) 7. Scalar Fluxes (17) 8. Scratch (18) 9. Scratch (19) 10. Direct Access (8) 11. Direct Access (9) 12. Activities (75) 13. Balances (76) 14. Input Dump (73) 15. Sensitivity Data (0) 16. Not Used (0) 17. Flux Guess (0) |
1$ - General Description [15] 1. IGE - geometry 2. IZM - number of zones 3. IM - number of intervals 4. IBL - left boundary condition 5. IBR - right boundary condition 6. MXX - number of mixtures 7. MS - mixing table length 8. ISN - angular quadrature 9. ISCT - order of scattering 10. IEVT - problem type 11. IIM - inner iteration maximum 12. ICM - outer iteration maximum 13. ICLC - optional theory 14. ITH - forward or adjoint 15. IFLU - GPT calculation flag |
DATA BLOCK 1 (continued) |
|
2$ - Editing and Control Options [10] 1. Fine-Group-Mixture Edit 2. Fine-Group-Flux Edit 3. Balance Table Edit 4. Broad-Group-Flux Edit 5. Not Used 6. Outers-Group-Limit-Option 7. Number of Bands 8. Suppress Fixed-Source Fission 9. Not Used 10. Not Used |
3$ - Other Options [12] 1. IFG - Weighting Option 2. IQM - Volumetric Sources 3. IPM - Boundary Sources 4. IFN - Starting Guess 5. ITMX - Time Shut-off 6. IDAT1 - Storage Scheme 7. IPN - Diff. Coeff. Option 8. IDFM - Density Factors 9. IAZ - Activities by Zone 10. IAI - Activities by Interval 11. IFCT - Thermal Scaling 12. IPVT - Search on k \(\neq\) 1 |
4$ - Weighting Options [9] 1. Type of weighting 2. Number of broad groups 3. Output format 4. Edit option 5. \(\sigma\)T position or number 6. \(\sigma\)gg position 7. Table length 8. ANISN edit option 9. Extra cross sections |
5* - Floating Point Values [12] 1. EPS - overall convergence 2. PTC - Point flux convergence 3. XNF - normalization 4. EV - starting guess for search 5. EVM - modifier for search 6. BF - buckling factor 7. DY - height 8. DZ - width 9. VSC - void streaming height 10. PV - k for search 11. EQL - search convergence 12. XNPM - search modifier T Terminate Data Block 1 |
Title Card - (18A4) |
DATA BLOCK 2 |
10$ CCCC Transport Cross Section Selector [IHTF] 11$ Composition numbers 12$ Additional Processes to be put on ANISN Library [MSCM] 13$ Mixture Numbers [MS] 14$ Isotope Identifiers [MS] 15* Isotope Concentrations [MS] 16$ CCCC Identifiers from Working Library [IHTF] 18U or 18# CCCC Identifiers on ISOTXS [IHTF] T Terminate the second Data Block. |
DATA BLOCK 3 |
{Required only when IQM or IPM is nonzero.} 30$ Spectrum Number by Interval (IQM>0) or Right-Hand Interval Boundary (IPM>0) [IM] 31* Volumetric Sources [IQM*IGM] 32* Boundary Sources [IPM*IGM*MM] T Terminate the third Data Block. |
DATA BLOCK 4 |
{When fluxes are read from an external device-IFN>3-this block is omitted.} 33# Flux Guess [IM*IGM] {IFN=0} 34# Fission Density Guess [IM] {IFN=1} T Terminate the fourth Data Block. |
Title Card - (18A4) |
DATA BLOCK 5 |
35* Interval Boundaries [IM + 1] 36$ Zone Numbers by Interval [IM] 38* Density Factors [IM] 39$ Mixture Number by Zone [IZM] 40$ Order of Scattering by Zone [IZM] 41* Radius Modifier by Zone [IZM] {IEVT=4} 42# Discrete-Ordinates Cosines [MM] 43# Discrete-Ordinates Weights [MM] 46$ Alternative Theory Selection [IGM] {ICLC>0} 47* Right-Boundary Albedos [IGM] 48* Left-Boundary Albedos [IGM] 49$ Activity Material or Nuclide Numbers [IAZ] 50$ Activity Process Numbers [IAZ] (See Appendix B) 51$ Broad-Group Numbers [IGM] {IFG>0} 52$ Lower-Band-Group Numbers [NBANDS] T Terminate the fifth Data Block. |
9.1.4. XSDRNPM Input/Output Assignments
The following logical units can be required in an XSDRNPM calculation.
Default Logical Unit |
Purpose |
|---|---|
3 |
Weighted Library (Produced by XSDRNPM) |
4 |
Working Library (Input) |
5 |
Card Input |
6 |
Standard Output |
7 |
Punch Fluxes or ANISN Libraries |
8 |
Scratch Direct-Access Device for External Cross-Section Storage |
9 |
Scratch Direct-Access Device for Mixing and Weighting Operations |
10 |
Scratch Direct-Access Device for External Flux Moment Storage |
16 |
Angular Fluxes |
17 |
Scalar Fluxes |
18 |
Scratch Device |
19 |
Scratch Device |
20 |
ANISN Binary Libraries or CCCC ISOTXS Interface |
31 |
Fundamental mode forward angular flux input unit for generalized adjoint calculation (iflu>0) |
32 |
Fundamental mode adjoint angular flux input unit for generalized adjoint calculation (iflu>0) |
73 |
Dump of Input and Derived Data |
75 |
Activities |
76 |
Balance Tables |
9.1.5. XSDRN Sample Problem
In this section, the input and output for a sample case involving a bare, homogeneous 16-cm sphere of a 93% enriched UO2-F2 solution is presented. The input AMPX working format cross-section library will be read from logical unit 4.
The input working library is a temporary 238-group library created by CSAS-mg containing the following nuclides:
Nuclide
Identifiera
235U92
92235
238U92
92238
1H
1001b
16O8
8016
19F9
9019
a These are the identifiers of the sets of data on the library created for the problem.
b Water-bound kernel.
An S16 quadrature is selected with 32 spatial intervals. Activities are requested for 235U92 absorption and fission and 238U92 absorption.
=xsdrn
93% uo2f2 solution sphere
1$$ 3 1 32 1 0 1 5 16 1 1 30 20 0 0 0
2$$ a7 -1 e
3$$ 1 a9 3 1 e
4$$ 0 4 0 -1 5 e
5** 1.-7 1.-8 e 1t
13$$ 1 1 1 1 1
14$$ 1001 8016 9019 92235 92238
15** 6.548-2 3.342-2 6.809-4 3.169-4 2.355-5
16$$ 1001 8016 9019 92235 92238
18## 6hh-1 6ho-16 6hf-19 6hu-235 6hu-238 2t
33## f1 4t
35** 31i0.0 16.0
36$$ f1
49$$ 92235 92235 92238
50$$ 18 27 27
51$$ 74r1 74r2 45r3 45r4 5t
end
9.1.6. Output Cross Sections
One of the most common uses of XSDRNPM is to collapse cross sections and write them onto a file for input into another computer code. At present, two options are allowed:
Output library in AMPX Working Library format. This library is always written when cross sections are collapsed.
Output library in ANISN binary or BCD format [XSDJD63]. The binary library is written on logical 20 by default; the BCD library is produced on logical 7. The identifiers on this library range from 1 to the total number of blocks required to accommodate the data.
9.1.7. Error messages
During the course of a problem, XSDRNPM makes many checks to determine if input data are in the required form. If inconsistencies are spotted, a message is printed, and the problem may be terminated. Some of these messages are listed below along with a brief description of their possible cause.
DATA N N arrays have been input with incorrect length. See the messages produced as arrays are read to determine specific arrays.
SN-1 N The Nth entry in the \(S_n\) quadrature directions is zero. (43# array)
SN-2 0 The \(S_n\) weights do not sum to 1.0. (42# array)
SN-3 0 The sum of the products of \(S_n\) weights and directions is not 0.0, that is, the directions are not symmetric. (42# and 43# arrays)
FIXS 0 Fixed source calculation requested (IEVT=0) and total fixed sources are zero.
Q-HI N A volumetric source spectrum numbered N has been requested where N is greater than IQM.
B-HI N A boundary source spectrum numbered N has been requested where N is greater than IPM.
FISS 0 IEVT\(\geq\) 1 and the total fission source is zero.
8101 N The Nth radius is negative.
8102 N The Nth radius is less than the (N-1)th radius.
8103 N Zone N dimensions have become negative in a zone width search.
MIX N A request has been made to use the Nth component from the mixing table, but this nuclide has not been requested from a library.
Several messages may be encountered during an XSDRNPM run which indicate problems with either the code or the setup:
ROOT L The polynomials from which the default angles are derived are incorrect.
BAND N The number of bands specified is greater than the number of groups.
WAT1 N The number of sets of weighted cross sections is incorrect.
WAT2 N The number of sets of weighted cross sections is incorrect.
*******************************************************INFACE************************************
*** WARNING YOU REQUESTED nn SETS OF CROSS SECTIONS, BUT ONLY mm SETS WERE FOUND *************
*******************************************************MIXEM*************************************
MAGIC WORD ERROR DETECTED IN MIXEM, MW= xx
*******************************************************SPOUT*************************************
NO PROGRAMMING PROVIDED FOR ITP= nn
*******************************************************FIDAS*************************************
****** ERROR nn ENTRIES REQUIRED IN xx? ARRAY
DATA EDIT CONTINUES
*******************************************************FIDAS*************************************
****** FILL OPTION IGNORED IN xx? ARRAY
*******************************************************FIDAS*************************************
****** WARNING ADDRESS aa IS BEYOND LIMITS OF xx? ARRAY
*******************************************************STORXS************************************
MAGIC WORD ERROR IN STORXS - GROUP gg MIXTURE mm L ln
MAGIC WORD mw IGI ig MXI mx MNI mn LLL 11
*******************************************************STORXS************************************
ERROR #1 IN STORXS.$
*******************************************************STORXS************************************
ERROR #2 IN STORXS.$
For the cryptic messages above (e.g., the last two), contact the code developers as to their possible cause.
References
- XSDAld63
Berni Alder. Methods in Computational Physics. V. 1. Academic Press, 1963.
- XSDCL65
B. G. Carlson and K. D. Lathrop. Discrete ordinates angular quadrature of the neutron transport equation. Technical Report LA-3186, Los Alamos National Laboratory, Los Alamos, NM (USA), 1965.
- XSDCar74
B. M. Carmichael. Standard interface files and procedures for reactor physics codes, version III. Technical Report, Los Alamos Scientific Laboratory, Los Alamos, NM (USA), 1974.
- XSDEme75(1,2,3,4)
B. B. Emett. The MORSE Monte Carlo Radiation Transport Code. Technical Report ORNL-4972, Oak Ridge National Laboratory, Oak Ridge, TN (USA), 1975.
- XSDEJ67
Ward W. Engle Jr. A User's Manual for ANISN: A One Dimensional Discrete Ordinates Code with Anisotropic Scattering. Technical Report, Oak Ridge Gaseous Diffusion Plant, Oak Ridge, TN (USA), 3 1967. Available from Radiation Shielding Information Center as CCC-82/ANISN.
- XSDGCJ69
N. M. Greene and C. W. Craven Jr. XSDRN: A DISCRETE ORDINATES SPECTRAL AVERAGING CODE. Technical Report, Union Carbide Corp. / Oak Ridge National Laboratory, Oak Ridge, TN (USA), 1969.
- XSDHTS76
H. Henryson, B. J. Toppel, and C. G. Stenberg. MC 2-2: a code to calculate fast neutron spectra and multigroup cross sections. Technical Report, Argonne National Laboratory, 1976.
- XSDHof82
T. J. Hoffman. The Optimization of Russian Roulette Parameters for KENO Va. Technical Report ORNL/TM-7539, Union Carbide Corp., Nucl. Div., Oak Ridge National Laboratory, Oak Ridge, TN (USA), 1982.
- XSDHT82
T. J. Hoffman and J. S. Tang. XSDRNPM-S biasing of MORSE-SGC/S shipping-cask calculations. Technical Report, Oak Ridge National Laboratory, Oak Ridge, TN (USA), 1982.
- XSDHon61
Henry C. Honeck. THERMOS. A Thermalization Transport Theory Code for Reactor Lattice Calculations. Technical Report, Brookhaven National Laboratory, Upton, NY, 1961.
- XSDJD63(1,2)
G. D. Joanou and J. S. Dudek. GAM-II. AB \$ sub 3\$ CODE FOR THE CALCULATION OF FAST-NEUTRON SPECTRA AND ASSOCIATED MULTIGROUP CONSTANTS. Technical Report, General Atomic Div., General Dynamics Corp., San Diego, Calif., 1963.
- XSDOls65
Tom Olsen. Void Streaming in Sn Calculations. Nuclear Science and Engineering (US), 1965.
- XSDREJ77
W. A. Rhoades and W. W. Engle Jr. New weighted-difference formulation for discrete-ordinates calculations. Technical Report, Oak Ridge National Laboratory, Oak Ridge, TN (USA), 1977.
- XSDRSCEJ79
W. A. Rhoades, D. B. Simpson, R. L. Childs, and W. W. Engle Jr. DOT-IV two-dimensional discrete ordinates transport code with space-dependent mesh and quadrature. Technical Report, Oak Ridge National Laboratory, Oak Ridge, TN (USA), 1979.
- XSDTREJ80
E. T. Tomlinson, W. A. Rhoades, and W. W. Engle Jr. Flux extrapolation models used in the DOT IV discrete ordinates neutron transport code. Technical Report, Oak Ridge National Laboratory, Oak Ridge, TN (USA), 1980.
- XSDWRHB79
C. R. Weisbin, R. W. Roussin, H. R. Hendrickson, and E. W. Bryant. Review of the theory and application of sensitivity and uncertainty analysis. Proceedings of a seminar-workshop, Oak Ridge, Tennessee. Technical Report, Oak Ridge National Laboratory, Oak Ridge, TN (USA), 1979.
- XSDWWCD15
D. Wiarda, M. L. Williams, C. Celik, and M. E. Dunn. AMPX-2000: A cross-section processing system for generating nuclear data for criticality safety applications. In Proc. Int. Conf. Nuclear Criticality Safety (ICNC 2015), Charlotte, North Carolina. 2015.
- XSDWil86
Mark L. Williams. Perturbation theory for nuclear reactor analysis. CRC Press, Inc., 1986.